La disequazione è una diseguaglianza che è verificata per certi intervalli di valori
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Una disequazione è una formula aperta con uno dei seguenti predicati: "essere minore", "essere minore o uguale", "essere maggiore", "essere maggiore o uguale".
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Anche per risolvere le disequazioni si utilizza un PRINCIPIO di EQUIVALENZA analogo a quello per le equazioni che può essere così riassunto.
Una disequazione si trasforma in una disequazione equivalente se:
si addiziona ( o si sottrae ) per lo stesso numero reale sia a sinistra, sia a destra del predicato;
si moltiplica ( o si divide ) per lo stesso numero reale positivo sia a sinistra sia a destra del predicato;
si moltiplica ( o si divide ) per lo stesso numero reale negativo sia a sinistra sia a destra del predicato; ma si inverte il predicato stesso
Soluzioni di una disequazione di I grado
Una disequazione ha, in genere, infinite soluzioni; è pertanto impossibile scriverle tutte.
Infatti anziché scriverle, si rappresentano graficamente.
Le soluzioni di una disequazione di primo grado in un'incognita sono in genere rappresentate da una semiretta.
Le soluzioni di una disequazione di primo grado in due incognite sono in genere rappresentate da un semipiano.
Disequazioni in una sola incognita
L'insieme delle soluzioni di una disequazione propria con predicato " < " oppure " > " può essere rappresentato con una semiretta aperta (senza cioè il suo estremo, indicato con una crocetta).
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Se invece, il predicato è " " oppure "
" oppure " " anche l'estremo della semiretta è soluzione e la sua rappresentazione è una semiretta chiusa (l'estremo si indicherà con un punto pieno).
" anche l'estremo della semiretta è soluzione e la sua rappresentazione è una semiretta chiusa (l'estremo si indicherà con un punto pieno).
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Disequazioni in due incognite
Abbiamo già anticipato che le soluzioni di una disequazione di primo grado in due incognite sono in genere rappresentate da un semipiano.
In maniera analoga alle disequazioni ad una sola incognita, a proposito delle frontiere si osserva quanto segue:
Se in una disequazione compaiono i predicati "minore" oppure "maggiore" il semipiano delle soluzioni è privo dei punti della retta di frontiera.
Se invece compaiono i predicati "minore o uguale" oppure "maggiore o uguale", anche i punti della retta di frontiera fanno parte dell'insieme delle soluzioni.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Sistemi di disequazioni di I grado
Risolvere un sistema di disequazioni significa trovare l’insieme dei numeri reali che sono soluzioni comuni alle disequazioni, cioè che verificano contemporaneamente tutte le disequazioni che compongono il sistema.
Per risolvere un sistema di disequazioni è sufficiente risolvere singolarmente ciascuna disequazione e poi considerare l' intersezione degli insiemi delle loro soluzioni: l'insieme risultante sarà l' insieme delle soluzioni del sistema e si indica con "I.S." .
Sistemi di disequazioni in una sola incognita
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Sistemi di disequazioni in due incognite
L'insieme delle soluzioni di un sistema di disequazioni di primo grado in due incognite è rappresentato dall'intersezione di più semipiani.
E' perciò una regione convessa del piano, se non è infinita o vuota, allora è un poligono.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





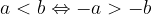
 " oppure "
" oppure " " anche l'estremo della semiretta è soluzione e la sua rappresentazione è una semiretta chiusa (l'estremo si indicherà con un punto pieno).
" anche l'estremo della semiretta è soluzione e la sua rappresentazione è una semiretta chiusa (l'estremo si indicherà con un punto pieno).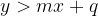 : semipiano superiore alla retta di equazione
: semipiano superiore alla retta di equazione 
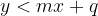 : semipiano inferiore alla retta di equazione
: semipiano inferiore alla retta di equazione 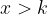 : semipiano a destra della retta
: semipiano a destra della retta 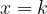
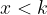 : semipiano a sinistra della retta
: semipiano a sinistra della retta 


