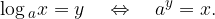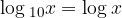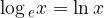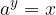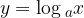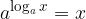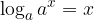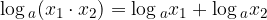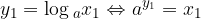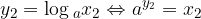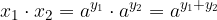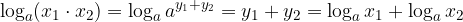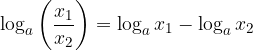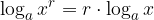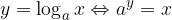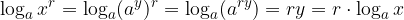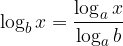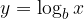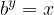Il logaritmo è l'operazione inversa dell'elevazione a potenza.
In Astronomia, ad esempio, la luminosità delle stelle, la magnitudine, viene calcolata in scala logaritmica. In chimica, i logaritmi sono utilizzati per determinare il pH delle soluzioni e in sismologia, sono utilizzati nella famosa scala Richter che determina l'intensità (magnitudo) dei terremoti. I logaritmi sono stati introdotti in astronomia perché semplificano i calcoli con grandi numeri, in particolare quando a piccole variazioni della variabile indipendente corrispondono variazioni molto elevate della variabile dipendente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Definizione
Cerchiamo di arrivare alla definizione di logaritmo a partire da un esempio:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Nell'esempio precedente, il valore di y non era difficile da trovare. Nella maggior parte dei casi però tale valore può essere determinato solo utilizzando il logaritmo.
Il logaritmo di un numero positivo x in base a, positiva e diversa da 1, è l'esponente y che bisogna dare alla base a per ottenere x:
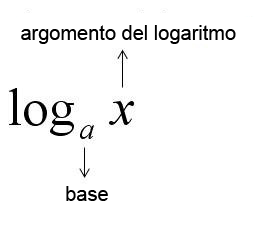
Gli elementi del logaritmo sono dunque:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Vediamo qualche altro esempio:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Logaritmi decimali
Si chiama logaritmo decimale un logaritmo in base 10.
Per convenzione, la base di un logaritmo decimale non si scrive:
Per calcolare un logaritmo decimale, possiamo aiutarci con una calcolatrice che solitamente contiene il tasto log.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Logaritmi naturali
Si chiama logaritmo naturale un logaritmo in base e.
Per convenzione, il logaritmo naturale viene scritto nel modo seguente:
Per calcolare un logaritmo naturale, possiamo aiutarci con una calcolatrice che solitamente contiene il tasto ln.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Operazioni aritmetiche con i logaritmi
Logaritmi e antilogaritmi
Abbiamo visto che il logaritmo è il processo attraverso il quale possiamo tradurre un'equazione esponenziale:
L'antilogaritmo è il processo attraverso il quale possiamo tradurre un'equazione logaritmica in un'equazione esponenziale.
Logaritmo e antilogaritmo sono dunque operazioni inverse.
Se combiniamo funzione logaritmica ed esponenziale nella stessa espressione in modo che il logaritmo sia esponente della funzione esponenziale o che la funzione esponenziale sia base del logaritmo, per ogni a > 0, avremo che:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Logaritmo di un prodotto
Il logaritmo del prodotto di numeri positivi è uguale alla somma dei logaritmi dei singoli fattori:
Il logaritmo di un prodotto equivale alla somma dei logaritmi:
Dimostriamo l'uguaglianza di cui sopra. Poniamo:
Se esprimiamo tale uguaglianza in forma logaritmica, avremo:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Logaritmo di un quoziente
Il logaritmo di un quoziente tra numeri positivi è uguale alla differenza tra il logaritmo del dividendo e il logaritmo del divisore.
Il logaritmo di un quoziente equivale alla differenza dei logaritmi:
La dimostrazione è simile a quella vista per il logaritmo di un prodotto.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Logaritmo di una potenza
Il logaritmo di una potenza è uguale al prodotto dell'esponente per il logaritmo della base della potenza.
Logaritmo di una potenza:
Dimostriamo quanto detto sapendo che:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Cambiamento di base
Abbiamo detto che spesso le calcolatrici consentono il calcolo dei logaritmi solo in base 10 o e. Se dobbiamo calcolare un logaritmo in base diversa, possiamo facilmente trasformarlo nel corrispondente logaritmo in base 10 o e. Vediamo come si procede:
Dato un logaritmo in base b, possiamo trasformarlo in un logaritmo in base a con la seguente formula:
Vediamo come si ottiene tale formula. Poniamo:
Partiamo dall'equazione esponenziale appena vista:
che è proprio la formula del cambiamento di base di un logaritmo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »