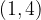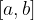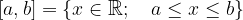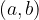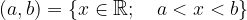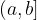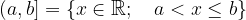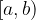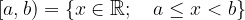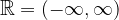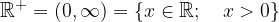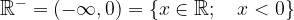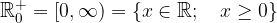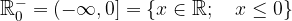Un intervallo è un insieme di numeri reali compresi tra due valori. Questi due numeri sono detti estremi dell'intervallo.
Un intervallo può essere rappresentato nel seguente modo:
Si tratta dell'insieme dei numeri compresi tra 1, detto estremo inferiore o sinistro dell'intervallo, e 4, detto estremo superiore o destro dell'intervallo.
Gli estremi possono essere compresi o esclusi dall'intervallo. Rappresentiamo:
con un cerchio pieno sulla retta reale gli estremi che sono compresi nell'intervallo;
con una punta di freccia gli estremi che non sono compresi nell'intervallo.
Un intervallo chiuso è formato da tutti i punti compresi tra gli estremi a e b, inclusi a e b; in questo caso gli estremi si scrivono tra parentesi quadre: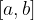 
Un intervallo chiuso è definito e rappresentato simbolicamente come segue:
Sulla retta reale un intervallo chiuso si rappresenta graficamente nel seguente modo:
I punti a e b sono compresi nell'intervallo.
Un intervallo aperto è formato da tutti i punti compresi tra gli estremi a e b, esclusi a e b; in questo caso gli estremi si scrivono tra parentesi tonde: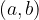 
Un intervallo aperto è definito e rappresentato simbolicamente come segue:
Sulla retta reale un intervallo aperto si rappresenta graficamente nel seguente modo:
I punti a e b non sono compresi nell'intervallo.
In questo caso possiamo distinguere i seguenti intervalli:
Questo intervallo è formato da tutti i punti compresi tra gli estremi a e b, con a escluso e b incluso; in questo caso l'estremo sinistro si racchiude tra parentesi tonda e l'estremo destro tra parentesi quadra: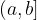 
Un intervallo aperto a sinistra e chiuso a destra è definito e rappresentato simbolicamente come segue:
Sulla retta reale questo tipo di intervallo si rappresenta graficamente nel seguente modo:
Il punto a non è compreso nell'intervallo e il punto b è compreso nell'intervallo.
Questo intervallo è formato da tutti i punti compresi tra gli estremi a e b, con a incluso e b escluso; in questo caso l'estremo sinistro si racchiude tra parentesi quadra e l'estremo destro tra parentesi tonda: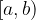 
Un intervallo chiuso a sinistra e aperto a destra è definito e rappresentato simbolicamente come segue:
Sulla retta reale questo tipo di intervallo si rappresenta graficamente nel seguente modo:
Il punto a è compreso nell'intervallo e il punto b non è compreso nell'intervallo.
Di seguito vedremo un esempio di come si determina un intervallo:
L'insieme dei numeri reali è un intervallo infinito.
L'insieme dei numeri reali può essere scritto sotto forma di intervallo nel seguente modo:
Possiamo scrivere in forma di intervallo anche i sottoinsiemi dei numeri reali:
Simbolicamente può essere scritto come:
Graficamente viene indicato come:
Simbolicamente può essere scritto come:
Graficamente viene indicato come:
Simbolicamente può essere scritto come:
Graficamente viene indicato come:
Simbolicamente può essere scritto come:
Graficamente viene indicato come:
