Il concetto di insieme è elementare e dobbiamo già poterlo intuire. Quando abbiamo degli oggetti, se riusciamo a considerarli collegati tra loro, abbiamo un insieme. La prima cosa da dire e' che gli oggetti (elementi) che compongono l'insieme devono sempre essere ben definiti prima ancora di considerare l'insieme stesso.
Un insieme è una collezione di oggetti, detti elementi dell'insieme.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Usiamo le lettere minuscole per definire gli elementi di un insieme e le lettere maiuscole per definire gli insiemi.
Possiamo dire l'elemento a appartiene all'insieme A.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Rappresentazione degli insiemi
Dobbiamo trovare un accordo per poter definire e rappresentare gli insiemi. Presentiamo varie strategie per poter rappresentare un insieme.
Elenco
Vengono elencati tutti gli elementi, tra parentesi graffe separati da virgole
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per insiemi infiniti, se risulta sufficientemente chiaro, si possono usare i puntini di sospensione.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Caratteristica
Si può definire la caratteristicha/proprietà che accomuna gli oggetti che compongono l'insieme
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
E' possibile specificare, negli insiemi numerici, a quale famiglia di numeri appartengano gli elementi, come numeri naturali, numeri interi, numeri razionali, numeri reali, numeri complessi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Diagrammi di Eulero Venn
In forma grafica mediante i diagrammi di Eulero Venn, rendendo gli insiemi visibili.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Si chiede che un insieme sia univocamente determinato. La sua definizione deve essere sempre molto chiara.
Non possiamo dire che A è l'insieme delle persone alte.
Possiamo dire invece che B è l'insieme delle persone più alte di 200 cm.
Si definisce cardinalità di un insieme il numero degli elementi di un insieme.
Operazioni con gli insiemi
Presentiamo le principali operazioni con gli insiemi.
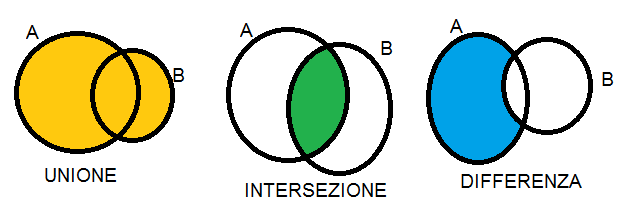
Unione, intersezione e differenza
Le principali operazioni tra insiemi sono:
L'unione di due insiemi A e B: si indica con 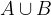 ed è l'insieme formato da tutti gli elementi di A e B presi una sola volta.
ed è l'insieme formato da tutti gli elementi di A e B presi una sola volta.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
L'intersezione di due insiemi A e B: si indica con 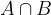 ed è data dall'insieme formato da tutti gli elementi che appartengono sia all'insieme A che all'insieme B contemporaneamente. L'intersezione tra l'insieme dei mesi e l'insieme delle parole che iniziano con la lettera N comprende solo novembre.
ed è data dall'insieme formato da tutti gli elementi che appartengono sia all'insieme A che all'insieme B contemporaneamente. L'intersezione tra l'insieme dei mesi e l'insieme delle parole che iniziano con la lettera N comprende solo novembre.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La differenza B meno A si indica con con 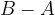 ed è data dall'insieme formato dai soli elementi di B che non appartengono ad A.
ed è data dall'insieme formato dai soli elementi di B che non appartengono ad A.
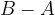 viene anche detto insieme complementare di A in B e si indica
viene anche detto insieme complementare di A in B e si indica 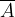 .
.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Operazioni con gli insiemi
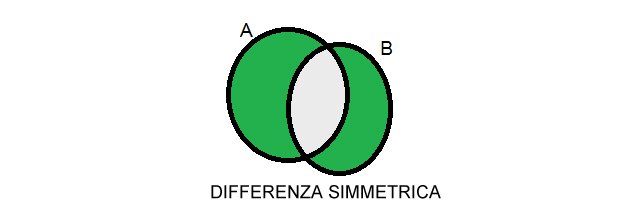
Differenza simmetrica
La differenza simmetrica tra due insiemi è l'insieme degli elementi che appartengono ad A e non a B oppure che appartengono a B e non ad A. Si indica con:
E' intuitivamente l'inverso dell'intersezione di due insiemi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Prodotto cartesiano
Insiemi particolari
Esistono alcuni insiemi particolari, definiti per alcune loro caratteristiche tipiche.
Sottoinsiemi
L'insieme dei pesci è un sottoinsieme del più vasto insieme degli animali. L'insieme degli Italiani è un sottoinsieme dell'insieme degli Europei.
In matematica, si dice che B è sottoinsieme di A se tutti i suoi elementi sono contenuti in A. Secondo tale definizione ogni insieme è contenuto in se stesso. Si usa la seguente notazione:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per ogni insieme possiamo trovare moltissimi sottoinsiemi. O molti insiemi che lo contengono.
Il concetto di sottoinsieme può essere legato al concetto di minore o uguale. Dire che B è sottoinsieme (anche coincidente) di A è ad intuito simile a dire che 3 è minore o uguale a 5.
Se invece si vuole escludere che B sia coincidente con A si usa la notazione seguente, similmente a come avviene per il minore.
Vediamo un altro esempio di sottoinsiemi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Insiemi disgiunti
Gli insiemi disgiunti non hanno alcun elemento in comune, come l'insieme dei vegetali e l'insieme degli animali.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Insieme vuoto
Si chiama insieme vuoto l'insieme che non contiene nessun elemento. Tale insieme si indica con il simbolo Ø oppure con due parentesi graffe consecutive, la prima aperta e l'altra chiusa 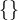 . L'insieme vuoto è sottoinsieme di qualsiasi altro insieme, incluso se stesso. Uno studente svogliato (che ha capito la teoria degli insiemi) potrebbe dire che l'insieme degli argomenti divertenti da studiare è un insieme vuoto.
. L'insieme vuoto è sottoinsieme di qualsiasi altro insieme, incluso se stesso. Uno studente svogliato (che ha capito la teoria degli insiemi) potrebbe dire che l'insieme degli argomenti divertenti da studiare è un insieme vuoto.
Insieme delle parti
Per qualunque insieme A esiste l'insieme delle parti o insieme potenza di A e si indica con:
E' l' insieme che ha come elementi tutti e soli i sottoinsiemi di A.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà delle operazioni con gli insiemi
Si possono combinare tra loro diverse operazioni tra gli insiemi e utilizzare le seguenti proprietà facilmente verificabili con degli esempi.
Proprietà distributiva dell'unione rispetto all'intersezione
L'unione di A con B intersecata con A è uguale all'unione dell'intersezione di A con B e di A con C.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà distributiva dell'intersezione rispetto all'unione
L'insieme A interescato all'unione di B e C è uguale all'unione dell'intersezione tra A e B e dell'intersezione tra A e C.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Legge di assorbimento di Boole
L'insieme A intersecato con l'unione di A e B è uguale ad A.
L'insieme A unito con l'intersezione di A e B è uguale ad A.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Le funzioni
Una funzione, anche detta applicazione, mappa o trasformazione, è definita dai seguenti oggetti:
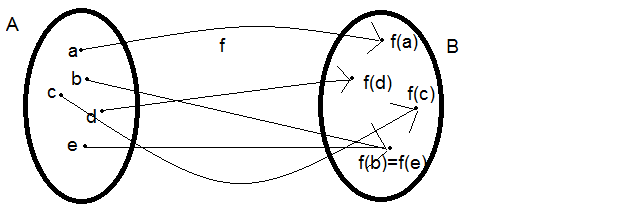
Rappresentazione di una funzione





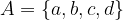
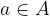
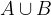 ed è l'insieme formato da tutti gli elementi di A e B presi una sola volta.
ed è l'insieme formato da tutti gli elementi di A e B presi una sola volta.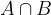 ed è data dall'insieme formato da tutti gli elementi che appartengono sia all'insieme A che all'insieme B contemporaneamente. L'intersezione tra l'insieme dei mesi e l'insieme delle parole che iniziano con la lettera N comprende solo novembre.
ed è data dall'insieme formato da tutti gli elementi che appartengono sia all'insieme A che all'insieme B contemporaneamente. L'intersezione tra l'insieme dei mesi e l'insieme delle parole che iniziano con la lettera N comprende solo novembre.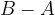 ed è data dall'insieme formato dai soli elementi di B che non appartengono ad A.
ed è data dall'insieme formato dai soli elementi di B che non appartengono ad A.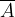 .
.
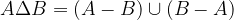
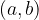 con
con 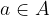 e
e 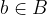
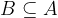
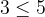
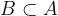
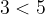
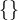 . L'insieme vuoto è sottoinsieme di qualsiasi altro insieme, incluso se stesso. Uno studente svogliato (che ha capito la teoria degli insiemi) potrebbe dire che l'insieme degli argomenti divertenti da studiare è un insieme vuoto.
. L'insieme vuoto è sottoinsieme di qualsiasi altro insieme, incluso se stesso. Uno studente svogliato (che ha capito la teoria degli insiemi) potrebbe dire che l'insieme degli argomenti divertenti da studiare è un insieme vuoto.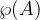
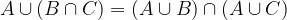
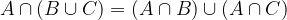
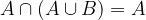
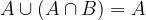
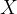 detto dominio della funzione
detto dominio della funzione 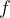 .
.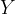 detto codominio della funzione
detto codominio della funzione 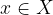 associa uno ed un solo elemento
associa uno ed un solo elemento 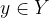 , indicandolo con
, indicandolo con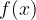 .
.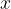 è l'argomento della funzione, oppure un valore della variabile indipendente, mentre
è l'argomento della funzione, oppure un valore della variabile indipendente, mentre 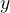 o
o 



