Se vogliamo determinare la posizione di un qualsiasi punto dobbiamo saper utilizzare il sistema di coordinate rettangolari (o sistema di coordinate cartesiane). Il punto si può trovare o nel piano o nello spazio a seconda del sistema di coordinate che si utilizza.
In questo capitolo ci concentriamo sui punti nello spazio.
Per trovare la loro posizione bisogna rappresentare i punti in un sistema di coordinate rettangolari, fissando un qualsiasi punto chiamandolo 0. Tale punto è detto origine.
Ora tracciamo tre linee che sono a due a due ortogonali e passano tutti per l'origine.
Orientiamo le tre linee del sistema, come mostra la figura.
Si stabilisce una unità di misura per tutte e tre le linee e si ottengono tre assi numerici.
I primi due assi sono gli stessi di quelli del piano: asse x o asse delle ascisse e asse y o asse delle ordinate; il terzo è chiamato asse z.
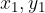La posizione di un punto T è scritta utilizzando tre coordinate 
e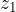 
:
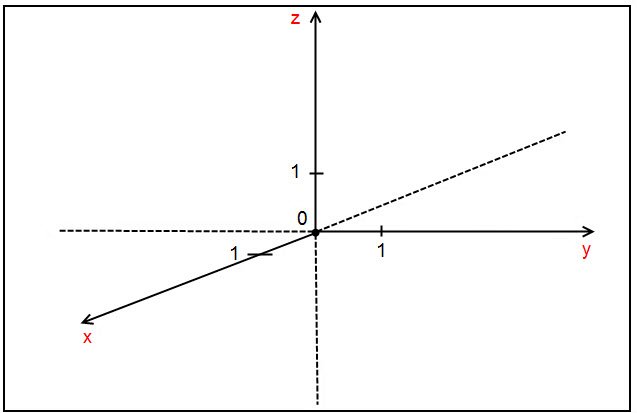
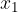è la prima coordinata di T e ci informa sulla sua posizione nell'asse x;
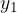è la seconda coordinata di T e ci informa sulla sua posizione nell'asse y;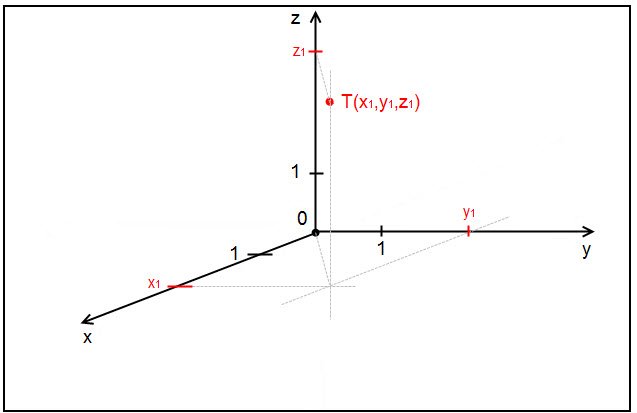
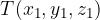è la terza coordinata di T e ci informa sulla sua posizione nell'asse z.
La posizione del punto T è scritta come una terna di coordinate 
. E' importante l'ordine con cui sono inserite le coordinate perchè, in caso contrario, si ottiene un punto dello spazio diverso da quello che si sarebbe voluto avere.
Vediamo un esempio di un punto ed una retta rappresentati nello spazio:
