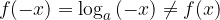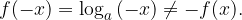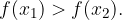Poiché una funzione esponenziale è biunivoca, esiste la sua funzione inversa.
La funzione inversa della funzione esponenziale è la funzione logaritmica con:
base a maggiore di 0 e diversa da 1;
argomento x maggiore di 0.
La base a di una funzione logaritmica non può essere 1, poiché in questo caso otterremmo una retta parallela all'asse delle ordinate di equazione x = 1, e dunque una funzione lineare.
Graficamente una funzione logaritmica si ottiene disegnando la curva simmetrica rispetto alla retta di equazione x=y della corrispondente funzione esponenziale.
Come per le funzioni esponenziali, le funzioni logaritmiche possono essere suddivise in due grandi famiglie a seconda del valore della base:
base maggiore di 1:
base compresa tra 0 e 1
Analizziamo le due famiglie con degli esempi concreti.
Adesso possiamo confrontare i grafici e le proprietà delle due funzioni. Entrambe le funzioni:
hanno lo stesso dominio, codominio e asintoto verticale
non sono né pari né dispari
passano per il punto (1, 0)
sono biiettive
sono speculari rispetto all'asse delle ascisse.
La prima funzione è tuttavia crescente e la seconda decrescente.
Dalla forma di una funzione logaritmica dipendono le sue proprietà e l'aspetto del suo grafico. Possiamo considerare due forme di funzione logaritmica, una forma canonica e una forma generale.
Sulla base delle loro proprietà comuni, possiamo definire la forma di funzioni logaritmiche del tipo:
come forma canonica delle funzioni logaritmiche. Si tratta di funzioni in cui il logaritmo non è moltiplicato per una costante e che non contengono un termine noto.
La forma generale di una funzione logaritmica è la seguente:
dove A determina l'espansione o la contrazione della curva lungo l'asse y (più grande è A, tanto più si spostano in alto i valori delle ordinate e viceversa), il valore di b determina lo spostamento della curva lungo l'asse x e il valore del termine noto c determina lo spostamento del grafico lungo l'asse y.
Se b < 0 il grafico si sposta di b unità verso sinistra, se b > 0 il grafico si sposta di b unità verso destra.
Se c < 0 il grafico si sposta di c unità verso il basso, se c > 0 il grafico si sposta di c unità verso l'alto.
Non dimentichiamo che quando spostiamo il grafico di una unità verso sinistra o destra, spostiamo di un'unità nello stesso verso anche l'asintoto verticale.
Come possiamo vedere, rispetto al grafico della forma canonica, la curva della funzione logaritmica in forma generale che abbiamo considerato presenta non solo un diverso asintoto verticale, ma non passa nemmeno per il punto (1, 0).
Poiché le proprietà delle funzioni logaritmiche sono diverse a seconda che la base sia maggiore di 1 o compresa tra 0 e 1, vedremo separatamente i due casi. Maggiore enfasi sarà data alle funzioni logaritmiche in forma canonica perché queste hanno caratteristiche comuni, indipendentemente dal valore della base a.
Le proprietà delle funzioni logaritmiche sono più semplici da capire se ne disegniamo e confrontiamo i grafici scegliendo diversi valori della base.
Il dominio di una funzione esponenziale diventa il codominio della relativa funzione logaritmica, mentre il codominio di una funzione esponenziale diventa il dominio della funzione logaritmica.
Le funzioni logaritmiche con base maggiore di 1 sono definite nell'insieme dei numeri reali positivi:
I valori assunti dalla funzione appartengono a tutto l'insieme dei numeri reali:
Dal grafico possiamo facilmente vedere che le funzioni logaritmiche con base a> 1 sono crescenti in tutto il loro campo di esistenza. Sappiamo che una funzione è strettamente crescente quando per ogni coppia di valori:
vale
Come possiamo vedere dal grafico, all'aumentare o al decrescere del valore della variabile x, la curva tende rispettivamente a più infinito e a meno infinito, il che vuol dire che non esistono un limite superiore e inferiore.
La funzione logaritmo non è limitata né superiormente né inferiormente.
Considerata una funzione logaritmica nella forma generale:
per valori di x infinitamente piccoli, la curva si approssima sempre di più all'asintoto verticale la cui equazione è data dal valore del coefficiente b:
Nel caso di funzioni logaritmiche in forma canonica, il coefficiente b=0 e quindi l'asintoto verticale è rappresentato dall'asse delle ordinate.
La costante A e il termine noto c non hanno alcuna influenza sull'asintoto verticale.
Ricordiamo che:
una funzione si dice iniettiva se ad ogni x distinta del dominio corrisponde una y distinta nel codominio.
una funzione si dice suriettiva se ogni elemento y del codominio è immagine di almeno un elemento x del dominio.
Una funzione è biiettiva, se è allo stesso tempo sia iniettiva che suriettiva.
Le funzioni logaritmiche sono biiettive e quindi invertibili (ovvero esiste la funzione inversa che è rappresentata dalla funzione esponenziale).
Tutte le funzioni logaritmiche in forma canonica intersecano l'asse delle ascisse in uno stesso punto che è il punto di coordinate (1, 0).
Nel caso delle funzioni logaritmiche in forma generale, il relativo grafico non passa per il punto (1, 0).
La funzione logaritmica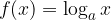 
non è pari perché:
La funzione logaritmica 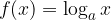non è dispari perché:
Come nella sezione precedente, considereremo anche qui diversi esempi in modo da descrivere più facilmente le proprietà di questa famiglia di funzioni logaritmiche. Maggiore enfasi sarà data alle funzioni logaritmiche in forma canonica perché queste hanno caratteristiche comuni, indipendentemente dal valore della base a.
Il dominio di una funzione esponenziale diventa il codominio della relativa funzione logaritmica, mentre il codominio di una funzione esponenziale diventa il dominio della funzione logaritmica.
Le funzioni logaritmiche con base compresa tra 0 e 1 sono definite nell'insieme dei numeri reali positivi:
I valori assunti dalla funzione appartengono a tutto l'insieme dei numeri reali:
Dal grafico possiamo facilmente vedere che le funzioni logaritmiche con base 0 < a < 1 sono decrescenti in tutto il loro campo di esistenza. Sappiamo che una funzione è strettamente decrescente quando per ogni coppia di valori:
vale
Come possiamo vedere dal grafico, all'aumentare o al decrescere del valore della variabile x, la curva tende rispettivamente a meno infinito e a più infinito, il che vuol dire che non esistono un limite superiore e inferiore.
La funzione logaritmo non è limitata né superiormente né inferiormente.
Considerata una funzione logaritmica nella forma generale:
per valori di x infinitamente piccoli, la curva si approssima sempre di più all'asintoto verticale la cui equazione è data dal valore del coefficiente b:
Nel caso di funzioni logaritmiche in forma canonica, il coefficiente b=0 e quindi l'asintoto verticale è rappresentato dall'asse delle ordinate.
La costante A e il termine noto c non hanno alcuna influenza sull'asintoto verticale.
Anche le funzioni logaritmiche con base compresa tra 0 e 1 sono biiettive e pertanto vale quanto affermato per le funzioni logaritmiche con base maggiore di 1.
Tutte le funzioni logaritmiche in forma canonica intersecano l'asse delle ascisse in uno stesso punto che è il punto di coordinate (1, 0).
Nel caso delle funzioni logaritmiche in forma generale, il relativo grafico non passa per il punto (1, 0).
La funzione logaritmica 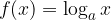non è pari perché:
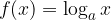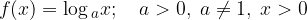
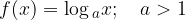
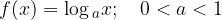
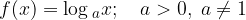
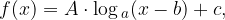
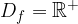
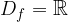
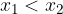
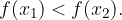
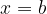
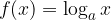La funzione logaritmica non è dispari perché:
