Immaginiamo una funzione continua come una curva che possiamo disegnare sul piano cartesiano senza staccare la matita dal foglio.
Definizione di funzione continua
Diamo una definizione matematica a quanto anticipato sopra.
Definizione di funzione continua in un punto.
Cioè se il limite della funzione nel punto coincide con la funzione valutata in quello stesso punto.
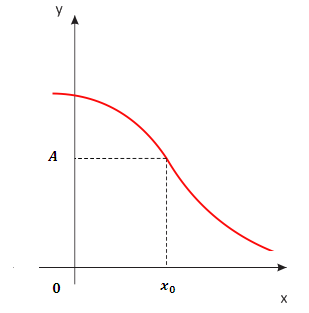
La funzione ha limite ed è continua in 
Osserviamo sotto un caso in cui la definizione non è soddisfatta, ovvero in cui troviamo un punto in cui la funzione non è continua. Il limite della funzione in  esiste ma è diverso dal valore della funzione valutata in quel punto. Infatti nel punto di ascissa
esiste ma è diverso dal valore della funzione valutata in quel punto. Infatti nel punto di ascissa  la funzione è spezzata e ha valore A.
la funzione è spezzata e ha valore A.
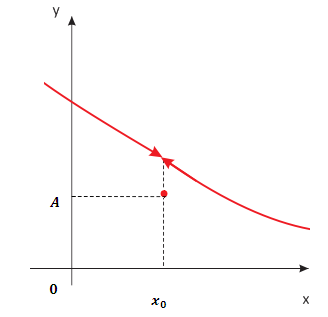
La funzione ha un limite diverso dal suo valore in 
Definizione di funzione continua in un intervallo.
Una funzione 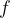 si dice continua in un intervallo
si dice continua in un intervallo 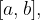 se è continua in ogni punto dell'intervallo.
se è continua in ogni punto dell'intervallo.
Limite sinistro e destro
Conosciamo già il concetto di limite. Vediamo ora quello di limite sinistro e limite destro.
Limite sinistro
Se la 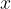 tende a
tende a  dalla parte sinistra, parliamo di limite sinistro.
dalla parte sinistra, parliamo di limite sinistro.
Il limite sinistro si rappresenta così: 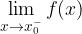
Diciamo che il limite sinistro della funzione 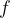 in
in  è il valore numerico A, o meglio che
è il valore numerico A, o meglio che
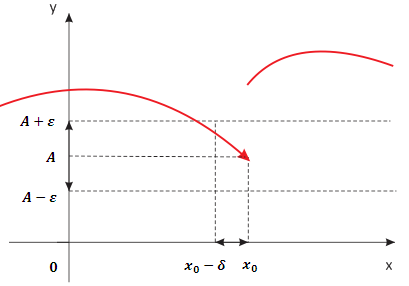
Limite sinistro: x si avvicina da sinistra
Limite destro
Se la 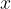 va a
va a  dalla parte destra, parliamo di limite destro.
dalla parte destra, parliamo di limite destro.
Il limite destro si rappresenta così: 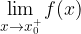
Diciamo che il limite destro della funzione 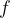 in
in  è il valore numerico A, o meglio che
è il valore numerico A, o meglio che
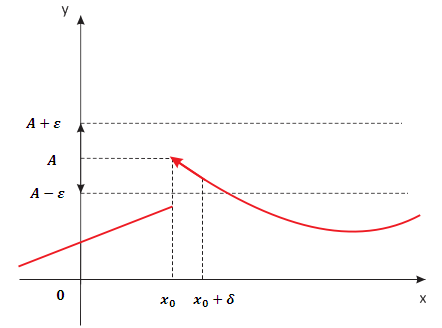
Limite destro: x si avvicina da destra
Relazione tra limite destro e sinistro
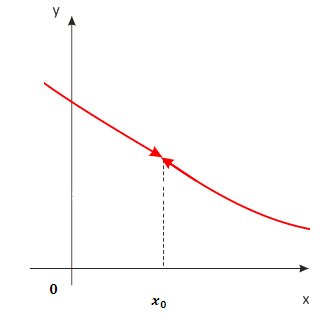
Perché il limite di una funzione in un punto sia definito, limite destro e limite sinistro devono esistere e coincidere.
Avvicinandosi a 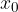 da destra o da sinistra, vediamo che i valori della funzione si avvicinano allo stesso valore (limite sinistro e destro sono gli stessi, quindi esiste il limite).
da destra o da sinistra, vediamo che i valori della funzione si avvicinano allo stesso valore (limite sinistro e destro sono gli stessi, quindi esiste il limite).
Punti di discontinuità
Possiamo avere punti di discontinuità quando una funzione è data da due funzioni differenti.
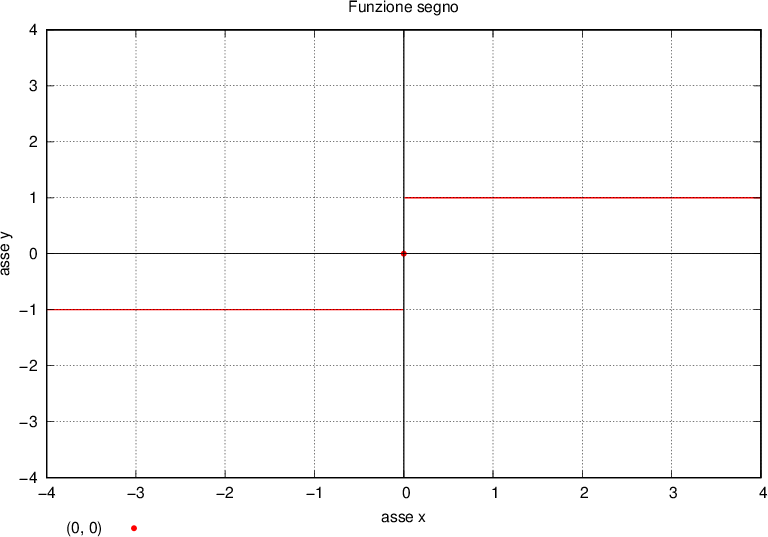
Prendiamo per esempio la funzione segno, che è definita come:
Tale funzione è definita ovunque, ma nel punto 0 non è continua, il grafico si interrompe.
Funzioni continue in tutto l'asse reale, definizioni
Alcuni funzioni continue, lo sono in tutto l'asse reale; eccole:
Funzione costante
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Funzione lineare
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Funzione quadratica
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Funzione potenza con esponente naturale
Funzione potenza con esponente naturale:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Funzione polinomiale
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Funzione esponenziale
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Funzione logaritmica
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Funzione seno
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Funzione coseno
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà delle funzioni continue
Di seguito vedremo alcune caratteristiche e proprietà delle funzioni continue.
Siano 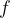 e
e 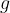 funzioni continue in un punto a. Allora:
funzioni continue in un punto a. Allora:
la loro somma (differenza) 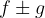 è una funzione continua nel punto a e vale la seguente regola:
è una funzione continua nel punto a e vale la seguente regola:
il loro prodotto 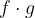 è una funzione continua nel punto a e vale la seguente regola:
è una funzione continua nel punto a e vale la seguente regola:
se g(a) è sempre diverso da zero, il loro quoziente 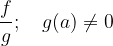 è una funzione continua nel punto a e vale la seguente regola:
è una funzione continua nel punto a e vale la seguente regola:
Vediamo altre proprietà e teoremi sulle funzioni continue.
Se la funzione 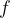 è continua e crescente, la sua funzione inversa
è continua e crescente, la sua funzione inversa 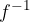 è anch'essa continua e crescente.
è anch'essa continua e crescente.
Teorema della permanenza del segno. Una funzione continua in un intervallo chiuso, che non si annulla mai in tale intervallo, ha segno costante in tutto l'intervallo (sempre positiva o sempre negativa).
Teorema degli zeri. Se la funzione è continua nell'intervallo chiuso 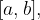 e assume valori di segno opposto agli estremi, allora in questo intervallo esiste almeno uno zero (cioè un punto in cui la funzione si annulla).
e assume valori di segno opposto agli estremi, allora in questo intervallo esiste almeno uno zero (cioè un punto in cui la funzione si annulla).
Se una funzione continua su un intervallo chiuso e limitato ha un limite superiore 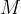 e un limite inferiore
e un limite inferiore 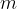 , allora assume tutti i valori intermedi compresi tra i due limiti superiore e inferiore.
, allora assume tutti i valori intermedi compresi tra i due limiti superiore e inferiore.





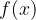 e un punto
e un punto  nel dominio, diciamo che la funzione è continua in
nel dominio, diciamo che la funzione è continua in 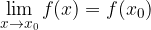


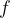 si dice continua in un intervallo
si dice continua in un intervallo 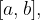 se è continua in ogni punto dell'intervallo.
se è continua in ogni punto dell'intervallo.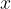 tende a
tende a  dalla parte sinistra, parliamo di limite sinistro.
dalla parte sinistra, parliamo di limite sinistro.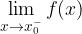
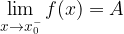
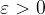 , esiste un
, esiste un 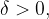 tale che per ogni
tale che per ogni 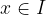 , con
, con 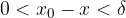 , risulta che
, risulta che 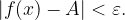
 sulle ordinate, esiste una distanza
sulle ordinate, esiste una distanza 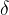 sulle ascisse legata ad essa tale che avvicinandoci a
sulle ascisse legata ad essa tale che avvicinandoci a 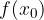 ).
).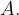 Pertanto il limite sinistro in
Pertanto il limite sinistro in 
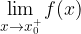
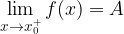
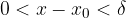 , risulta che
, risulta che 
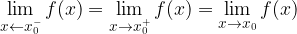
 da destra o da sinistra, vediamo che i valori della funzione si avvicinano allo stesso valore (limite sinistro e destro sono gli stessi, quindi esiste il limite).
da destra o da sinistra, vediamo che i valori della funzione si avvicinano allo stesso valore (limite sinistro e destro sono gli stessi, quindi esiste il limite).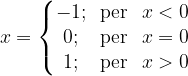
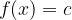
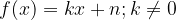
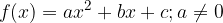
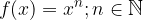
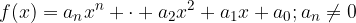
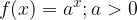
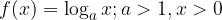
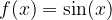
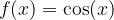
 funzioni continue in un punto a. Allora:
funzioni continue in un punto a. Allora: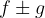 è una funzione continua nel punto a e vale la seguente regola:
è una funzione continua nel punto a e vale la seguente regola: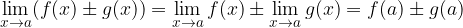
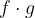 è una funzione continua nel punto a e vale la seguente regola:
è una funzione continua nel punto a e vale la seguente regola: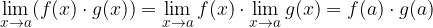
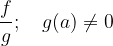 è una funzione continua nel punto a e vale la seguente regola:
è una funzione continua nel punto a e vale la seguente regola: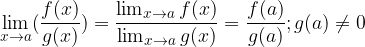
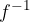 è anch'essa continua e crescente.
è anch'essa continua e crescente.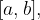 e assume valori di segno opposto agli estremi, allora in questo intervallo esiste almeno uno zero (cioè un punto in cui la funzione si annulla).
e assume valori di segno opposto agli estremi, allora in questo intervallo esiste almeno uno zero (cioè un punto in cui la funzione si annulla).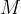 e un limite inferiore
e un limite inferiore 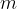 , allora assume tutti i valori intermedi compresi tra i due limiti superiore e inferiore.
, allora assume tutti i valori intermedi compresi tra i due limiti superiore e inferiore.


