Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





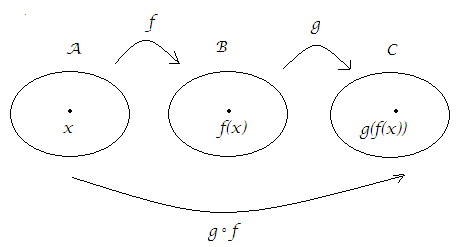
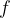 e
e 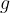
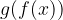
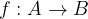
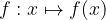
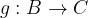
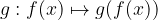
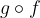
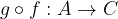
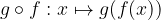
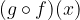
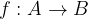 si dice invertibile se esiste una funzione
si dice invertibile se esiste una funzione 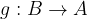 tale che:
tale che: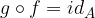
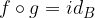
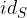 rappresenta la funzione identità su
rappresenta la funzione identità su 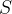 .
.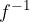 .
.


