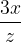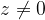Una frazione algebrica è il quoziente di due espressioni algebriche intere dette termini della frazione algebrica e di cui, come per le frazioni numeriche, il termine dividendo è denominato numeratore e il termine divisore è denominato denominatore.
In particolare, però, ciò che distingue una frazione algebrica da una frazione numerica è che, mentre in una frazione numerica, numeratore e denominatore sono numeri interi relativi, in una frazione algebrica avremo:
il numeratore che può essere rappresentato da un numero intero relativo, da un monomio o, nel caso più complesso, da un polinomio.
e il denominatore che deve necessariamente essere rappresentato da un monomio o da un polinomio.
Dunque, perché sia tale, una frazione algebrica deve sempre presentare una parte letterale al denominatore.
Tenendo presente che un quoziente non cambia se si moltiplicano o si dividono sia il dividendo che il divisore per lo stesso numero diverso da zero, anche per le frazioni algebriche vale la cosiddetta proprietà invariantiva per cui:
Una frazione algebrica non cambia se si moltiplicano o si dividono entrambi i suoi termini per uno stesso numero, lettera o espressione algebrica.
Inoltre, trattandosi di quozienti, anche le frazioni algebriche non possono avere un denominatore nullo e pertanto, per le lettere che compaiono al denominatore, vanno sempre esclusi tutti i valori che lo renderebbero nullo.
Il denominatore deve essere diverso da 0
In questa frazione il valore di z NON può essere nullo! Altrimenti l'espressione non ha significato.
Quando numeratore e denominatore di una frazione algebrica hanno un fattore comune, dividendo entrambi i termini per tale fattore si ottiene una frazione algebrica equivalente che si dice semplificata.
Una frazione algebrica è detta irriducibile o ridotta ai minimi termini quando il suo numeratore e il suo denominatore non hanno alcun fattore in comune. Dividendo i termini di una frazione algebrica per il loro M.C.D., si ottiene una frazione irriducibile, cioè ridotta alla più semplice espressione ottenibile.
E' possibile ridurre al minimo comune denominatore due o più frazioni algebriche irriducibili, trovando il m.c.m. dei denominatori che verrà assunto come denominatore comune per tutte le frazioni. Il numeratore di ognuna delle frazioni, invece, sarà ottenuto moltiplicando quest'ultimo per il quoziente ottenuto dalla divisione del m.c.m. trovato per il relativo denominatore.
La somma algebrica di frazioni algebriche che abbiano lo stesso denominatore è data da una frazione algebrica che ha per denominatore, il denominatore comune, e per numeratore, la somma algebrica dei numeratori.
Qualora le frazioni non avessero lo stesso denominatore, si procede prima alla riduzione al minimo comun denominatore come visto precedentemente.
Il prodotto di frazioni algebriche è dato da una frazione algebrica il cui numeratore è il prodotto dei numeratori e il cui denominatore è il prodotto dei denominatori.
Il quoziente di due frazioni algebriche è dato da una frazione algebrica che si ottiene moltiplicando la prima frazione per l'inversa della seconda.
Due frazioni si dicono inverse o reciproche quando il numeratore di ognuna di esse è denominatore dell'altra.
La potenza ad un determinato esponente di una frazione algebrica è data da una frazione algebrica che ha per numeratore e denominatore le potenze, a quel dato esponente, del numeratore e denominatore rispettivamente.
Conoscendo ora tutte le operazioni algebriche razionali che possiamo effettuare sui monomi, polinomi e frazioni algebriche, è possibile svolgere qualsiasi espressione algebrica razionale in cui tali operazioni siano presenti.
