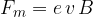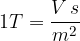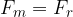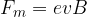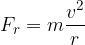Linee di campo
Il campo magnetico è un campo vettoriale dove un corpo carico, subisce una forza magnetica con intensità che dipende dalla sua distanza dal magnete.
Le linee di campo possono essere individuate posizionando degli aghi magnetici in prossimità della calamita: essi si disporranno parallelamente al campo, individuando la sua direzione. Le linee di campo sono chiuse, escono dal polo Nord ed entrano nel polo Sud del magnete
Linee di campo di un magnete permanente
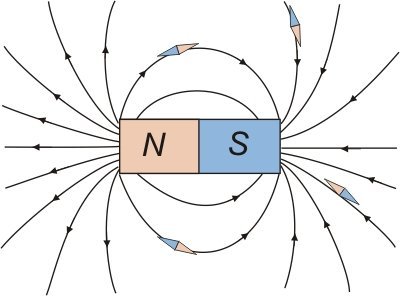
Forza che agisce su una carica in presenza di un campo magnetico
La forza magnetica agisce solo su particelle cariche in movimento. La sua intensità è proporzionale alla velocità della particella e al valore della sua carica oltre che al campo magnetico.
L'equazione della forza magnetica su una carica in movimento (in modulo), detta Forza di Lorentz, è la seguente:
L'unità di misura del campo magnetico è il Tesla (T) che è uguale a:
La direzione della forza di Lorentz è ortogonale al piano formato dal campo magnetico e dalla velocità della particella. Il verso è dato dalla regola della mano destra.
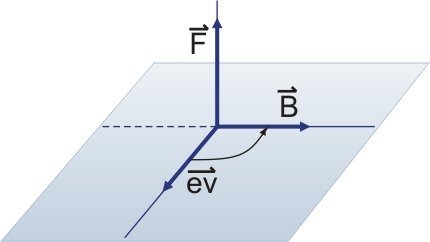
Rappresentazione della forza magnetica che agisce su una carica in movimento
Come abbiamo visto sopra il vettore della forza magnetica è ortogonale alla velocità della particella. Nella figura successiva vediamo che è possibile determinare la direzione della forza con la regola della mano sinistra: portiamo le dita delle mani in direzione della velocità e le chiudiamo nel verso opposto a cui va il campo magnetico. La direzione del pollice indicherà la direzione e il verso della forza magnetica
Solitamente usiamo il cerchio con una croce per indicare un vettore o un campo entranti nello schermo
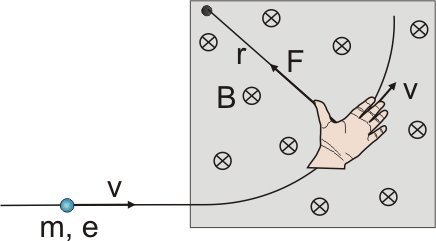
Moto di una particella carica in un campo magnetico
Raggio di curvatura
Dato che la forza è di tipo centripeta, è possibile definire il raggio di curvatura nel seguente modo
Svolgiamo questa equazione per ricavare r:
redattore del materiale didattico: Paolo Rota