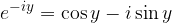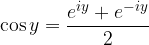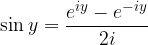Nei capitoli precedenti abbiamo visto come è possibile rappresentare un numero complesso in un piano cartesiano in cui in ascissa ed in ordinata si pongono rispettivamente la parte reale e la parte immaginaria del numero complesso. Tale rappresentazione è chiamata geometrica. Le altre due rappresentazioni di cui parleremo sono la forma trigonometrica e la forma esponenziale.
Forma trigonometrica dei numeri complessi
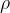 rappresenta la lunghezza del segmento OP
rappresenta la lunghezza del segmento OP
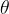 rappresenta l'angolo tra l'asse delle ascisse ed il segmento OP (calcolato in senso antiorario)
rappresenta l'angolo tra l'asse delle ascisse ed il segmento OP (calcolato in senso antiorario)
La forma trigonometrica con cui si esprime un numero complesso è la seguente:
dove, in particolare si ha:
Le ultime due formule possono essere scritte in forma compatta come:
Queste sono le formule che permettono di passare dalla forma algebrica alla forma trigonometrica. Per passare dalla forma trigonometrica a quella algebrica:
Nella forma trigonometrica l'argomento 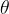 si può esprimere in gradi oppure in radianti. Se, ad esempio, conosciamo l'angolo in gradi (30°), la formula per passare ai radianti è:
si può esprimere in gradi oppure in radianti. Se, ad esempio, conosciamo l'angolo in gradi (30°), la formula per passare ai radianti è:
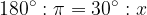 da cui si otterrebbe
da cui si otterrebbe 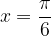
Se, invece, conosciamo l'angolo in radianti (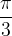 ), la formula per passare ai gradi è:
), la formula per passare ai gradi è:
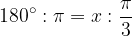 da cui si otterrebbe
da cui si otterrebbe 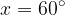
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Operazioni tra numeri complessi espressi in forma trigonometrica
Analogamente alla rappresentazione in forma algebrica, nella forma trigonometrica è possibile definire le operazioni di moltiplicazione, divisione e potenza; inoltre è possibile calcolare la radice n-ma. Prima di vedere una per una le operazioni, introduciamo il concetto di reciproco di un numero complesso espresso in forma trigonometrica
Dato il numero complesso 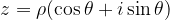 , il suo reciproco
, il suo reciproco  ha come modulo il reciproco del modulo del numero dato e come argomento l'opposto dell'argomento del numero considerato
ha come modulo il reciproco del modulo del numero dato e come argomento l'opposto dell'argomento del numero considerato
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Moltiplicazione
Il prodotto tra due numeri complessi espressi in forma trigonometrica è un numero complesso che ha per modulo il prodotto dei moduli dei fattori e per argomento la somma degli argomenti dei fattori.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La regola vale anche nel caso di moltiplicazione di tre o più numeri complessi espressi in forma trigonometrica.
In generale, quindi, il modulo si otterrà moltiplicando i moduli di tutti i fattori, mentre l'argomento si otterrà sommando tutti gli argomenti dei fattori.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Divisione
La divisione tra due numeri complessi espressi in forma trigonometrica, di cui il secondo diverso da zero, è un numero complesso che ha per modulo il quoziente dei moduli dei numeri e per argomento la differenza degli argomenti del dividendo e del divisore.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Potenza
Effettuare la potenza vuol dire applicare per 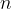 volte la proprietà del prodotto di un numero complesso per sè stesso.
volte la proprietà del prodotto di un numero complesso per sè stesso.
Si perviene alla cosiddetta Formula di Moivre:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La Formula di Moivre si può applicare anche nel caso di esponente negativo. In tal caso la formula diventa:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Radice n-ma
Se il numero complesso è espresso nella forma trigonometrica 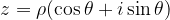 , allora esso ammette n radici ennesime che si ottengono dalla seguente formula:
, allora esso ammette n radici ennesime che si ottengono dalla seguente formula:
nella quale si pone, via via, 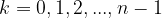
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Forma esponenziale dei numeri complessi
Per definire la forma esponenziale occorre introdurre una importante funzione della variabile complessa, cioè la funzione esponenziale.
Se consideriamo la variabile complessa 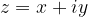 , per definizione si ha:
, per definizione si ha:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Se si pone 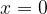 si ottiene la prima formula di Eulero:
si ottiene la prima formula di Eulero:
A questo punto passiamo a definire la forma esponenziale dei numeri complessi.
Dato il numero complesso 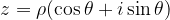 , applicando la prima formula di Eulero, si ottiene la forma esponenziale:
, applicando la prima formula di Eulero, si ottiene la forma esponenziale:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Sostituendo al posto di 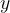 il valore
il valore 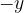 , si ottiene la seconda formula di Eulero:
, si ottiene la seconda formula di Eulero:
Combinando, infine, la prima e seconda formula di Eulero si ottengono la terza e quarta formula di Eulero:
E' bene specificare che tutte le proprietà delle funzioni esponenziali si applicano anche al caso della forma esponenziale dei numeri complessi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





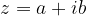 si può rappresentare graficamente utilizzando le coordinate polari attraverso il modulo
si può rappresentare graficamente utilizzando le coordinate polari attraverso il modulo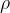 e l'argomento (o anomalia)
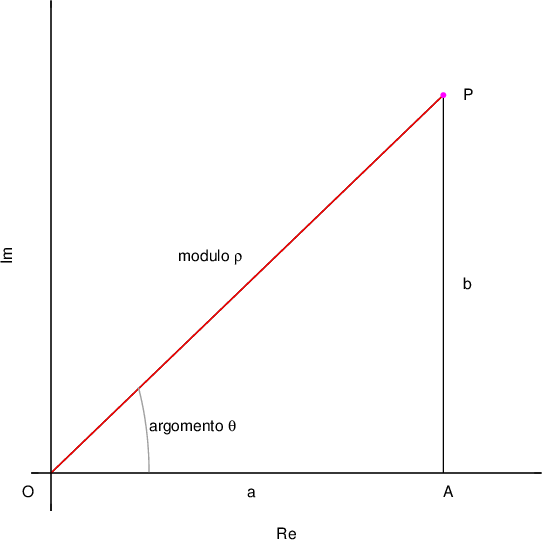
e l'argomento (o anomalia)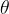 .
.
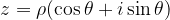
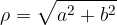
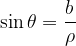
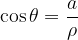
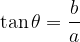
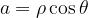
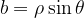
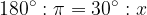 da cui si otterrebbe
da cui si otterrebbe 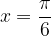
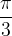 ), la formula per passare ai gradi è:
), la formula per passare ai gradi è: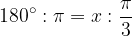 da cui si otterrebbe
da cui si otterrebbe 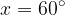
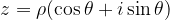 , il suo reciproco
, il suo reciproco  ha come modulo il reciproco del modulo del numero dato e come argomento l'opposto dell'argomento del numero considerato
ha come modulo il reciproco del modulo del numero dato e come argomento l'opposto dell'argomento del numero considerato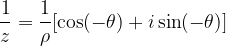
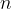 volte la proprietà del prodotto di un numero complesso per sè stesso.
volte la proprietà del prodotto di un numero complesso per sè stesso.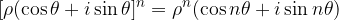
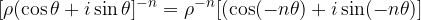
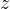 e un numero positivo intero
e un numero positivo intero 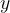 tale che:
tale che: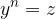
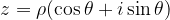 , allora esso ammette n radici ennesime che si ottengono dalla seguente formula:
, allora esso ammette n radici ennesime che si ottengono dalla seguente formula: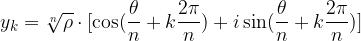
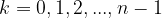
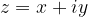 , per definizione si ha:
, per definizione si ha: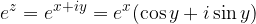
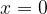 si ottiene la prima formula di Eulero:
si ottiene la prima formula di Eulero: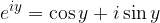
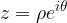
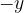 , si ottiene la seconda formula di Eulero:
, si ottiene la seconda formula di Eulero: