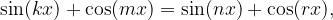Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





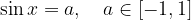
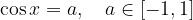
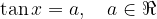
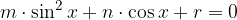
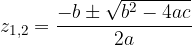
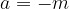
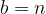
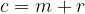
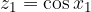
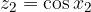
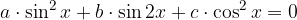
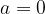 oppure
oppure 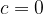 , l'equazione si può scomporre in fattori.
, l'equazione si può scomporre in fattori.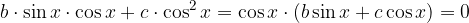
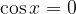
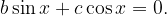
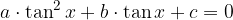
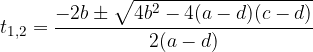
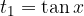
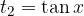
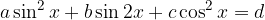
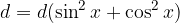 .
.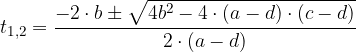
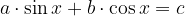
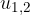 , ci resta ancora da risolvere
, ci resta ancora da risolvere