In questo capitolo parleremo delle equazioni razionali e delle disequazioni razionali, ossia di quelle equazioni e disequazioni che derivano da uguaglianze e disuguaglianze tra funzioni razionali.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Definizioni
Consideriamo due funzioni razionali, espresse come
Di esse ci interessa conoscere:
l'intersezione, ossia risolvere la equazione razionale
gli intervalli della x in cui il valore della prima funzione è maggiore (o è minore) rispetto al valore della seconda; in altre parole risolvere la disequazione razionale
Si definisce equazione razionale l'uguaglianza tra due funzioni razionali nella quale si devono calcolare i valori di x che la soddisfano, ossia i punti in cui i relativi grafici delle funzioni si intersecano.
La disequazione razionale.
Si definisce disequazione razionale la disuguaglianza tra due funzioni razionali, a prescindere dal segno di maggiore > o minore <, nella quale si devono calcolare l'intervallo delle x dove il valore della prima funzione è maggiore o minore del valore della seconda, a seconda del segno richiesto.
Equazioni razionali
Date le funzioni razionali:
Se vogliamo trovare i punti di intersezione delle due funzioni razionali è sufficiente scrivere:
Calcolare queste intersezioni significa risolvere una equazione razionale.
Quindi stiamo cercando i valori di x, per cui sia valida l'espressione suddetta. Possiamo così riscriverla:
Tale espressione è uguale a 0 quando il numeratore è uguale a 0 ed il denominatore è diverso da 0.
Siamo quindi alla ricerca di soluzioni per l'equazione:
ma che, allo stesso tempo, non coincidano con le soluzioni dell'equazione:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Soluzioni dell'equazione razionale.
Data l'equazione razionale nella forma 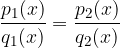 , una volta semplicata nella forma equivalente
, una volta semplicata nella forma equivalente 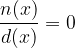 , le soluzioni dell'equazione sono gli tutti gli zeri del numeratore esclusi gli zeri del denominatore.
, le soluzioni dell'equazione sono gli tutti gli zeri del numeratore esclusi gli zeri del denominatore.
Disequazioni razionali
Consideriamo le due funzioni razionali
Quando ricerchiamo i valori di x per cui il valore della funzione razionale f(x) è minore del valore della funzione razionale g(x), diciamo che dobbiamo risolvere la disequazione razionale:
Il nostro compito è dunque quello di trovare le x per cui la disequazione razionale è soddisfatta.
Facciamo qualche passaggio:
Affinchè sia verificata quest'ultima disequazione numeratore e denominatore devono avere segno discorde (uno positivo, l'altro negativo o viceversa), inoltre il denominatore deve essere diverso da 0.
Si applica una delle due opzioni dei segni discordi.
Esattamente nello stesso modo come stiamo cercando una soluzione per:
si trovano soluzioni alle seguenti:
Diamo un'occhiata a tutte le combinazioni e alle loro soluzioni:
Le disequazioni possono essere risolte con la retta dei reali o con i grafici. Vediamo un esempio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Soluzioni della disequazione razionale 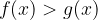 con il metodo grafico.
con il metodo grafico.
Soluzioni della disequazione razionale 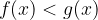 con il metodo grafico.
con il metodo grafico.





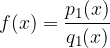
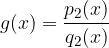
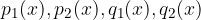 sono polinomi dipendenti da x e
sono polinomi dipendenti da x e 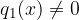 ,
, 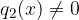 .
.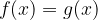
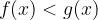
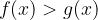
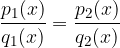
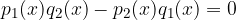
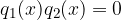
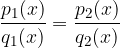 , una volta semplicata nella forma equivalente
, una volta semplicata nella forma equivalente 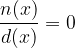 , le soluzioni dell'equazione sono gli tutti gli zeri del numeratore esclusi gli zeri del denominatore.
, le soluzioni dell'equazione sono gli tutti gli zeri del numeratore esclusi gli zeri del denominatore.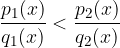
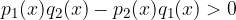
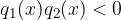
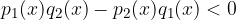
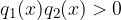
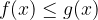
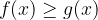
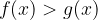 usando la retta dei reali.
usando la retta dei reali.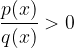 viene risolta unendo le soluzioni ottenute da
viene risolta unendo le soluzioni ottenute da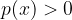 e
e 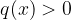
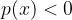 e
e 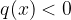 .
.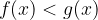 usando la retta dei reali.
usando la retta dei reali.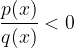 viene risolta unendo le soluzioni ottenute da
viene risolta unendo le soluzioni ottenute da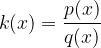 sta al di sopra dell'asse delle ascisse.
sta al di sopra dell'asse delle ascisse.


