Si chiama equazione di primo grado un'uguaglianza in cui grado massimo delle incognite (ossia le lettere di cui si deve determinare il valore) è pari a 1:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esistono equazioni di grado superiore al primo, come quelle di secondo grado.
Ciò che si trova a sinistra dell’uguale è detto primo membro, ciò che si trova a destra è detto secondo membro. Tale uguaglianza può diventare vera sostituendo alla lettera (incognita) un valore particolare detto soluzione.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Risolvere un'equazione di primo grado
I valori dell’incognita che soddisfano la equazione sono detti soluzioni o radici dell’equazione.
Due equazioni si dicono equivalenti quando tutte le soluzioni della prima sono anche soluzioni della seconda e viceversa.
Due equazioni equivalenti a una terza sono equivalenti tra loro.
In generale per risolvere un’equazione si cerca di trasformarla in un’altra ad essa equivalente, ma di forma più semplice.
Per far ciò si utilizzano i principi di equivalenza.
1° principio di equivalenza
Sommando o sottraendo ad entrambi i membri di una equazione una stessa espressione si ottiene una equazione equivalente a quella data.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Da tale principio derivano le seguenti regole, spiegate tramite esempi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
2° principio di equivalenza
Moltiplicando o dividendo ambo i membri di una equazione per una stessa espressione (diversa da zero) si ottiene una equazione equivalente a quella data.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Da tale principio derivano le seguenti regole, spiegate tramite esempi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Le equazioni di primo grado intere
Le equazioni di primo grado intere sono quelle in cui l’incognita si trova solo al numeratore.
Il procedimento utilizzato per risolvere questo tipo di equazioni è il seguente:
Procedimento per risolvere un'equazione di primo grado:
Si spostano i termini con la 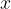 a 1° membro e quelli senza la
a 1° membro e quelli senza la 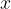 a secondo membro.
a secondo membro.
I termini che si spostano da un membro all'altro devono essere cambiati di segno, quelli che non si spostano restano con lo stesso segno.
Si sommano i termini simili.
Si dividono ambo i membri per il numero davanti alla 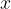 .
.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Le equazioni di primo grado fratte
Le equazioni di primo grado fratte sono quelle in cui l’incognita si trova al denominatore.
Bisogna ricordare in questo caso che:
E' assolutamente vietato dividere un numero per 0
Bisogna quindi escludere dalle possibili soluzioni tutti i valori che annullano il denominatore.
Il procedimento utilizzato per risolvere questo tipo di equazioni è il seguente:
Si scompongono in fattori i denominatori.
Si determina un denominatore comune.
Si leva il denominatore e si calcola il campo di esistenza.
Bisogna indicare con 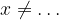 quali sono i valori della
quali sono i valori della 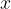 che annullano il denominatore.
che annullano il denominatore.
Per fare ciò si pone il denominatore diverso da zero.
Si spostano i termini con la 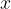 a primo membro e quelli senza la
a primo membro e quelli senza la 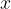 a secondo membro.
a secondo membro.
I termini che si spostano devono essere cambiati di segno, quelli che non si spostano restano con lo stesso segno.
Si sommano i termini simili.
Si dividono ambo i membri per il numero davanti alla 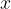 .
.
Si verifica che la soluzione non sia una di quelle escluse con il campo di esistenza.
Se la soluzione è una di quelle escluse l’equazione è impossibile.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Equazioni indeterminate
Si definisce indeterminata un'equazione che si presenta sotto la forma 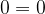 , nella quale tutti i valori possibili della
, nella quale tutti i valori possibili della 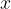 sono soluzioni.
sono soluzioni.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Equazioni impossibili
Si definisce impossibile un'equazione che si presenta sotto la forma 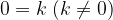 , in questo caso infatti nessun valore della
, in questo caso infatti nessun valore della 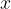 è soluzione.
è soluzione.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Equazioni letterali
Le equazioni letterali sono quelle in cui compaiono altre lettere oltre all'incognita, del tipo:
Il procedimento è lo stesso utilizzato per risolvere le equazioni intere e fratte.
Ci sono però due differenze:
Nel risultato spesso ci sono delle lettere al denominatore. In questi casi bisogna discutere la soluzione.
Quando risolviamo un'equazione letterale è importante tener presente che il parametro occupa il posto di un numero, dunque per risolvere l'equazione bisogna tener presente che non è possibile dividere per zero; quindi al posto della lettera non si potranno sostituire quei numeri che rendono il denominatore pari a zero.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





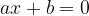
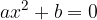
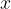 a 1° membro e quelli senza la
a 1° membro e quelli senza la 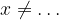 quali sono i valori della
quali sono i valori della 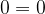 , nella quale tutti i valori possibili della
, nella quale tutti i valori possibili della 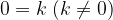 , in questo caso infatti nessun valore della
, in questo caso infatti nessun valore della 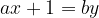
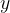 ,
, 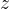 sono utilizzate per indicare le incognite, mentre le lettere
sono utilizzate per indicare le incognite, mentre le lettere 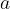 ,
, 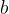 ,
, 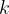 vengono usate per indicare i parametri, vale a dire dei simboli che possono essere sostituiti da numeri.
vengono usate per indicare i parametri, vale a dire dei simboli che possono essere sostituiti da numeri.


