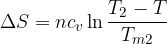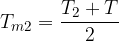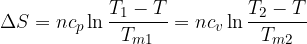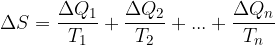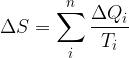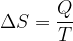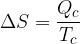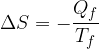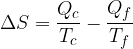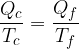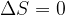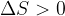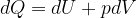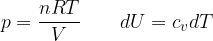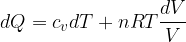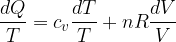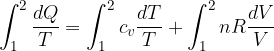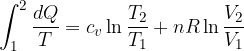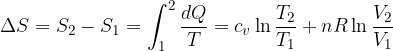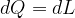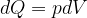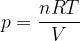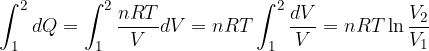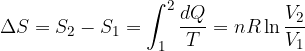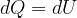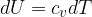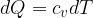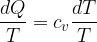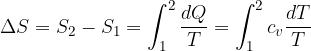Il concetto di entropia è stato introdotto da Clausius nel XIX secolo per descrivere la caratteristica di un sistema nel quale le trasformazioni avvengono in direzione del maggior disordine.
Riportiamo quanto scrisse a riguardo in un suo trattato:
"Possiamo dire che S [l'entropia] indica il contenuto di trasformazione del corpo, così come diciamo che U [l'energia interna] è il contenuto di calore e lavoro del corpo stesso. [...] Propongo di chiamare la grandezza S con il nome di entropia, partendo dalla parola greca tropè che significa trasformazione. Intenzionalmente ho formato il termine entropia in modo da renderlo il più possibile simile al termine energia: infatti entrambe queste quantità sono così strettamente connesse l'una all'altra dal punto di vista del significato fisico, che mi pare utile una certa analogia anche nei loro nomi."
Il termine entropia infatti deriva dal greco ed è formato dal suffisso "eu", dentro,e da "tropè", cambiamento, trasformazione. Il termine energia invece, dal greco "energheia", composto dal solito suffisso "eu", dentro) e da "ergon", capacità di agire.
I concetti di energia ed entropia sintetizzano i due principi della termodinamica: l'energia totale di un sistema isolato si conserva, mentre l'entropia aumenta sempre.
Clausius definì l'entropia come il rapporto tra la quantità di calore scambiata e la temperatura durante lo scambio:
Tale termine non è altro che una funzione di stato che dipende solamente dallo stato fisico caratterizzato dalle coordinate termodinamiche p, V, T.
L'entropia è una funzione di stato e viene indicata con S.
La variazione di entropia per una trasformazione reversibile vale:
L'entropia S si misura in [Joule/Kelvin].
In parole molto semplici quindi possiamo interpretare l'entropia come il grado di disordine di un sistema. Un aumento del disordine implica un aumento dell'entropia. Cerchiamo di chiarire con degli esempi:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Questi due esempi significano che in natura l'aumento di entropia è spontaneo mentre non avverrà mai spontaneamente una diminuzione dell'entropia.
E' possibile ridurre l'entropia di un sistema, ma solamente fornendo al sistema lavoro dall'esterno. Questo processo comporta comunque un aumento dell'entropia dell'ambiente e quindi dell'universo. Facciamo alcuni esempi:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Trasformazioni irreversibili e reversibili
Come abbiamo già visto esistono trasformazioni reversibili e irreversibili.
La maggior parte delle trasformazioni in natura sono possibili solo in una direzione, sono cioè irreversibili.
Le trasformazioni reversibili, avvengono in entrambe le direzioni, ma c'è bisogno di lavoro esterno.
L'entropia è una funzione di stato molto importante per distinguere quali trasformazioni sono reversibili e quali non lo sono.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Le trasformazioni reversibili sono solitamente quelle che avvengono molto lentamente, senza attrito e in qualsiasi momento del processo il sistema è in equilibrio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La maggior parte delle trasformazioni è irreversibile in natura. Sono possibili trasformazioni reversibili se:
il corpo alla fine del ciclo torna nello stesso stato da cui è partito
gli stati intermedi sono identici nell'una e nell'altra direzione
durante la trasformazione non c'è attrito o resistenza dell'aria
i cambiamenti avvengono lentamente in modo che tutte le parti del sistema siano sempre in equilibrio termico (trasformazione quasi-statica).
L'entropia nelle trasformazioni
L'entropia è una funzione di stato, e come per tutte le funzioni di stato, la relativa variazione è nulla per un gas che compie una trasformazione ciclica, mentre dipende solo dallo stato iniziale e da quello finale per una trasformazione aperta.
Per quanto riguarda l'Universo (cioè sistema + ambiente) il secondo principio della termodinamica dice che per ogni trasformazione termodinamica deve valere la relazione:
dove vale l’uguaglianza solo per trasformazioni reversibili.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Vediamo come calcolare la variazione di entropia nelle trasformazioni reversibili:
trasformazione adiabatica
In una trasformazione adiabatica non c'è scambio di calore, perciò non c'è variazione di entropia:
Riscaldamento/raffreddamento isobaro reversibile
Se una sostanza viene riscaldata o raffreddata in modo reversibile e non avviene alcun passaggio di stato si ha che la variazione di entropia è:
Riscaldamento/raffreddamento isocoro reversibile
Analogamente la variazione di entropia correlata ad un riscaldamento o a un raffreddamento a volume costante è:
Trasformazione isoterma reversibile
Se una sostanza subisce una trasformazione a temperatura costante la sua energia interna non varia, perciò:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Sul diagramma di Clapeyron le curve che definiscono le adiabatiche indicano anche che l'entropia è costante.
Se vogliamo disegnare un fascio di isotermiche è sufficiente variare T, come si fa a tracciare un fascio di adiabatiche?
Una possibilità è quella di effettuare una trasformazione irreversibile nel gas, e aumentarne l'entropia. Un calcolo di questo tipo però è abbastanza complicato, ma se la trasformazione avviene in modo reversibile a volume o a pressione costante possiamo facilmente calcolare il valore della variazione.
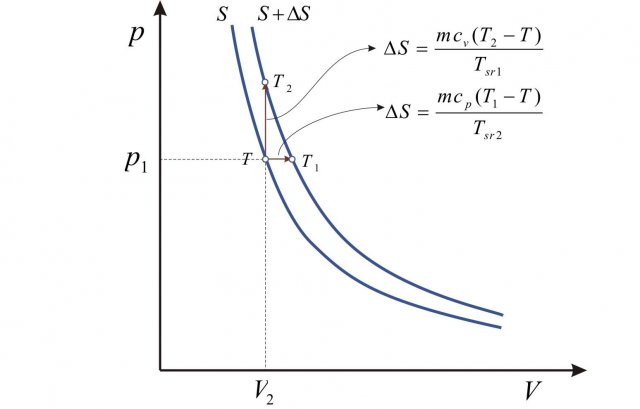
Figura 3:trasformazione isocora e isobara tra due adiabatiche
Dall'adiabatica possiamo compiere una trasformazione isobara per aumentare l'entropia considerando uno stato intermedio a temperatura 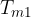 :
:
Oppure dall'adiabatica possiamo compiere una trasformazione isocora per aumentare l'entropia considerando uno stato intermedio a temperatura 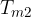 :
:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Un calcolo più preciso dell'entropia implica che il passaggio tra uno stato e un altro sia piccolo, e che la variazione di entropia sia la somma delle piccole variazioni consecutive, cioè:
e scritto in forma più sintetica:
Se la differenza di temperatura tra due stati è grande, possiamo comunque calcolare l'entropia utilizzando la temperatura media, ma per un calcolo più preciso dobbiamo suddividere l'intervallo in sottointervalli e per ciascuno calcolare la variazione di entropia.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
L'entropia e il ciclo di Carnot
Abbiamo visto che il ciclo di Carnot è formato da due isoterme e due adiabatiche e lo abbiamo tracciato sul diagramma di Clapeyron. Esiste anche un altro diagramma, chiamato diagramma entropico, in cui il ciclo di Carnot risulta di più immediata lettura. In questo nuovo diagramma abbiamo la temperatura e l'entropia come assi coordinati.
Le adiabatiche diventano delle isoentropiche (delle rette verticali) e le isoterme delle rette orizzontali, il ciclo è perciò rappresentato da un rettangolo.
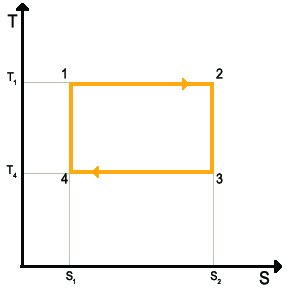
Diagramma entropico del ciclo di Carnot
1-2: isoterma - 
2-3: isoentropica (adiabatica) - 
3-4: isoterma - 
4-1: isoentropica (adiabatica) - 
Il calore scambiato dalle adiabatiche reversibili è nullo, perciò la variazione di entropia è data solo dalle isoterme, secondo la:
Dove Q è il calore ed equivale al lavoro (dato che per una isoterma la variazione di energia interna è nulla). Quindi per la prima isoterma vale:
Per convenzione il segno negativo indica l calore ceduto dal sistema.
Quindi la variazione di entropia nel ciclo vale:
perciò, per un ciclo reversibile:
Calcolo dell'entropia con gli integrali
Questo paragrafo è dedicato a chi volesse approfondire il calcolo dell'entropia, quanto è già stato esposto è comunque sufficiente per affrontare gli esercizi sull'argomento.
In una trasformazione reversibile un gas perfetto assorbe una quantità infinitesima di calore, dQ. Secondo il primo principio il calore è legato alla variazione di energia interna e al lavoro secondo la:
Per un gas perfetto possiamo sostituire:
Questa espressione non è integrabile ma se dividiamo entrambi i membri per T otteniamo:
Quindi se il sistema viene portato da uno stato 1 a uno stato 2 secondo una trasformazione reversibile possiamo ottenere la somma, cioè l'integrale di dQ/dT:
Il primo termine non è altro che la variazione di entropia:
L'entropia nelle trasformazioni isoterme
Dal primo principio della termodinamica sappiamo che per una trasformazione isoterma (temperatura costante) si ha:
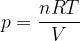
e integriamo tra gli stati 1 e 2
Calcoliamo l'entropia come:
L’entropia aumenta quando il sistema compie lavoro, quindi aumenta durante le espansioni (dV>0) isotermiche, sia reversibili che irreversibili.
L'entropia diminuisce durante le compressioni (dV<0) isotermiche reversibili. Per diminuire l’entropia di un sistema si deve compiere lavoro sul sistema.
Vediamo un esempio per il calcolo dell'entropia nelle trasformazioni isoterme:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
L'entropia nelle trasformazioni isocore
Dal primo principio della termodinamica sappiamo che per una trasformazione isocora si ha:
L'energia interna in questo caso è pari a:
Se dividiamo per T ricaviamo l'espressione dell'entropia:
integriamo tra gli stati 1 e 2:
L’entropia aumenta riscaldando un corpo (dT>0) a volume costante sia mediante una trasformazione reversibile che irreversibile
L’entropia diminuisce raffreddando un corpo (dT<0) a volume costante mediante una trasformazione reversibile
Riprendiamo l'esempio del capitolo precedente e risolviamolo con gli integrali:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »




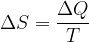

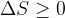
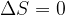
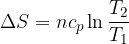
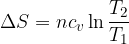
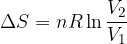

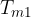 :
: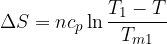
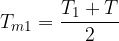
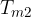 :
: