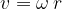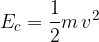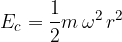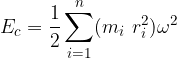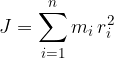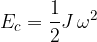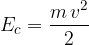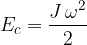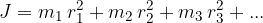L'energia cinetica (dal greco antico kinesis, movimento) è l'energia che un corpo possiade quando ha una certa velocità.
Più precisamente, l’energia cinetica che possiede un corpo di massa m è pari al lavoro necessario per portarlo da una velocità iniziale nulla alla velocità finale v.
Tale energia dipende quindi dalla massa e dalla velocità del corpo.
Viene abitualmente indicata con 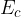 e si esprime con la stessa unità di misura del lavoro, il Joule [J].
e si esprime con la stessa unità di misura del lavoro, il Joule [J].
L’espressione per calcolarla è:
L'energia cinetica di un corpo
Come possiamo ricavare l’espressione dell’energia cinetica?

Fig. 1: Energia cinetica di un'automobile
L’automobile grigia è ferma (velocità nulla) e nessuna forza agisce su di essa. L'energia cinetica in questo caso è zero.
Sull'automobile arancione invece agisce una forza F e si muove a una velocità v. Secondo Newton l’auto, sotto l’azione di forze esterne F costanti, si muove con moto uniformemente accelerato con accelerazione pari ad a.
Calcoliamo lo spazio s percorso dall'automobile al tempo t:
Calcoliamo poi il lavoro compiuto dalla forza F nello spazio s:
La forza, secondo Newton, è pari alla massa per l’accelerazione:
Per trovare l'espressione dell'energia cinetica sostituiamo nell'espressione di L le espressioni di F e di s:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
L'energia cinetica è l'energia che possiede un corpo di massa m quando si muove ad una velocità v:
È una grandezza scalare e ha la stessa unità di misura del lavoro: il Joule [J].
Teorema dell'energia cinetica
Consideriamo ancora l'automobile arancione che sotto l'azione di una forza F si muove da un punto A a un punto B percorrendo uno spazio s.

Figura 2: La macchina percorre uno spazio s da A a B
Nel punto A ha una velocità 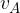 , in B ha una velocità
, in B ha una velocità 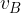 , l'energia cinetica in A è data quindi da:
, l'energia cinetica in A è data quindi da:
Il teorema dell'energia cinetica (o teorema delle forze vive) afferma che il lavoro della forza applicata è uguale alla variazione di energia cinetica del corpo.
Se il lavoro è positivo significa che la forza che agisce nella stessa direzione dello spostamento (l'energia cinetica aumenta).
Se il lavoro è negativo invece significa che la forza che agisce nella direzione opposta al movimento del corpo (l'energia cinetica del corpo diminuisce)
Il Teorema può essere anche espresso in altri termini.
Se un corpo possiede un'energia cinetica iniziale 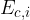 e una forza F agisce su di esso effettuando un lavoro L, l'energia cinetica finale
e una forza F agisce su di esso effettuando un lavoro L, l'energia cinetica finale 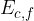 del corpo è uguale alla somma dell'energia cinetica iniziale e del lavoro compiuto dalla forza lungo la traiettoria del moto:
del corpo è uguale alla somma dell'energia cinetica iniziale e del lavoro compiuto dalla forza lungo la traiettoria del moto:
Il Teorema dell'energia cinetica dice che il lavoro della forza applicata è pari alla variazione di energia cinetica del corpo:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
L'energia cinetica di rotazione
Consideriamo un corpo rigido, un corpo cioè che non si deforma durante il movimento. Il moto di un corpo rigido non vincolato può essere:
di traslazione (come nell'esempio precedente)
di rotazione intorno ad un asse
una composizione tra i due tipi di moto precedenti
Consideriamo il caso di un corpo rigido di massa m che ruoti intorno a un asse fisso. Dato che il corpo è rigido le particelle che lo compongono mantengono la loro distanza dall'asse e quindi mantengono anche la stessa velocità. In questo caso la velocità che consideriamo è la velocità angolare 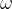 , che non è altro che la velocità di rotazione del corpo.
, che non è altro che la velocità di rotazione del corpo.
Consideriamo un punto generico del corpo distante r dall'asse di rotazione, la sua velocità tangenziale è data da:
Dato che il punto ha una certa velocità, allora possiede anche energia cinetica.
Scriviamo l'espressione dell'energia cinetica:
e sostituiamo alla velocità v l'espressione in funzione della velocità angolare 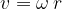 :
:
L'espressione precedente è l'energia cinetica di un punto appartenente a un corpo in rotazione, l'energia cinetica di tutto il corpo è data quindi dalla somma dei contributi di tutte le particelle che lo compongono:
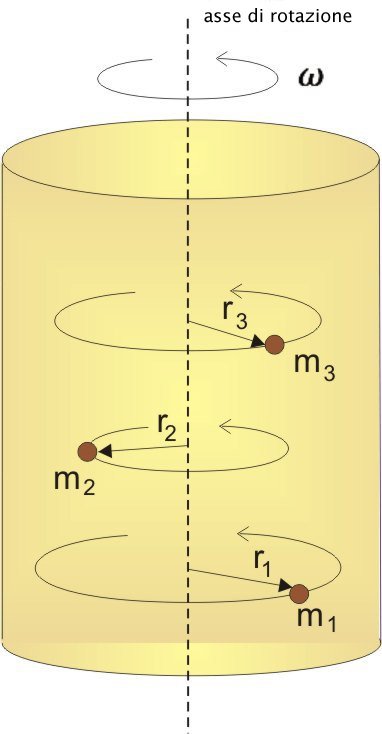
Figura 3: Energia cinetica di rotazione
Occorre definire ora una nuova grandezza chiamata momento d'inerzia J:
Sostituiamo nell'equazione dell'energia cinetica e otteniamo:
L'energia cinetica di un corpo in moto rotatorio dipende dalla velocità angolare e dal momento d'inerzia:
Il momento d'inerzia J è costante per un corpo rigido dato l'asse di rotazione.
Osservazione
Confrontiamo le due espressioni dell'energia cinetica, la prima per il moto di traslazione, la seconda per il moto rotatorio:
La massa m nella prima equazione rappresenta una caratteristica del corpo: maggiore la massa e più elevata è l'inerzia (la resistenza alle variazioni dello stato di moto) del corpo.
Analogamente il momento d'inerzia J nella seconda equazione: maggiore J, maggiore l'inerzia.
La differenza fondamentale tra l'inerzia nel moto traslatorio, che dipende solo dalla massa, e l'inerzia nel moto rotatorio è che in quest'ultimo l'inerzia dipende dal momento d'inerzia, cioè dalla massa e dalla sua posizione rispetto all'asse di rotazione, vale a dire dipende dalla configurazione geometrica del corpo.
Il momento d'inerzia di un corpo composto
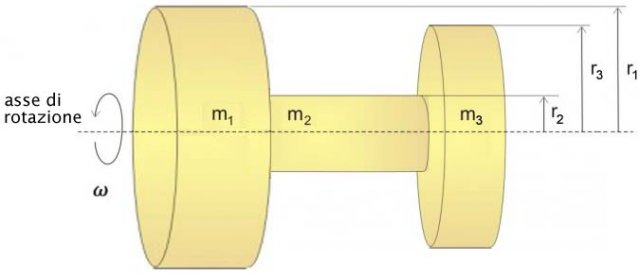
Figura 4: Corpo composito
Il momento d'inerzia di un corpo composito si ottiene sommando i momenti di inerzia di ogni massa elementare:
Nella maggior parte dei casi, il calcolo dei momenti di inerzia richiede l'uso degli integrali, ma per alcune forme semplici il calcolo è immediato, vediamo alcuni esempi in tabella:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »




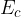 e si esprime con la stessa unità di misura del lavoro, il Joule [J].
e si esprime con la stessa unità di misura del lavoro, il Joule [J].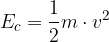

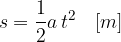
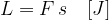
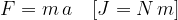
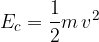

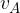 , in B ha una velocità
, in B ha una velocità 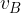 , l'energia cinetica in A è data quindi da:
, l'energia cinetica in A è data quindi da: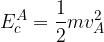
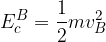
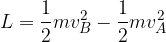
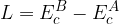
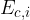 e una forza F agisce su di esso effettuando un lavoro L, l'energia cinetica finale
e una forza F agisce su di esso effettuando un lavoro L, l'energia cinetica finale 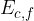 del corpo è uguale alla somma dell'energia cinetica iniziale e del lavoro compiuto dalla forza lungo la traiettoria del moto:
del corpo è uguale alla somma dell'energia cinetica iniziale e del lavoro compiuto dalla forza lungo la traiettoria del moto: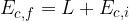
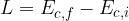
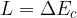
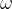 , che non è altro che la velocità di rotazione del corpo.
, che non è altro che la velocità di rotazione del corpo.