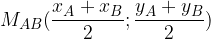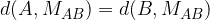Distanza tra due punti nel piano

Misurare la distanza tra due punti è un'operazione semplice. Anche nella vita di tutti i giorni misuriamo la distanza tra due oggetti.

Possiamo misurare la distanza tra due punti nel piano cartesiano a partire dalle loro coordinate.

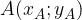Calcolare la distanza fra due punti e 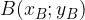nel piano cartesiano equivale a calcolare la lunghezza del segmento AB che li separa. Vediamo prima il caso particolare, in cui i due punti sono allineati agli assi cartesiani. Passiamo poi al caso generico.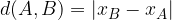

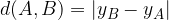
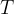Vediamo, attraverso degli esempi, due casi particolari in cui i punti sono allineati agli assi.

Vediamo ora il caso più generale, con due punti qualsiasi.

Rappresentiamo nel piano cartesiano due punti generici e .

Rappresentiamo un terzo punto di coordinate .

Dal disegno vediamo che il triangolo ATB è un triangolo rettangolo, il che significa che è possibile applicare il teorema di Pitagora per calcolare la lunghezza del segmento AB.

Le misure dei cateti sono le lunghezze dei segmenti AT e BT:

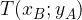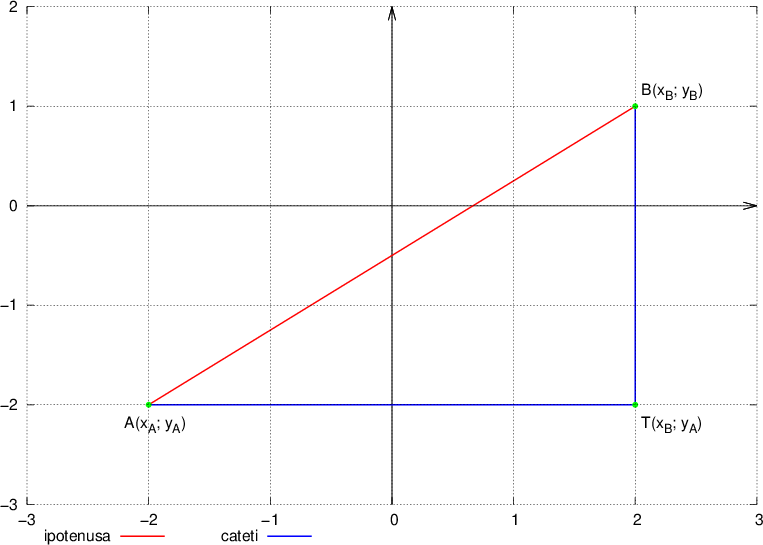
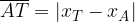
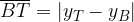
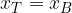Vediamo dal disegno che e 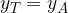. Possiamo quindi scrivere, sostituendo alle precedenti.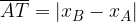

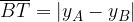
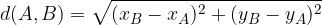
Il punto T non è quindi necessario per calcolare la distanza tra A e B. Calcoliamo la distanza.

Sfruttiamo il teorema di Pitagora per calcolare la lunghezza dell'ipotenusa AB:

Vediamo la definizione di punto medio.

Il punto medio del segmento AB ha per coordinate la media aritmetica delle coordinate di A e B. Si trova in mezzo al segmento, cioè ha la stessa distanza dai due estremi: