Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





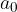 e del coefficiente del termine di grado massimo
e del coefficiente del termine di grado massimo 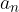 . Nel caso in cui il coefficiente di grado massimo sia 1, i potenziali zeri sono interi.
. Nel caso in cui il coefficiente di grado massimo sia 1, i potenziali zeri sono interi.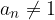 , allora il potenziale zero è un numero razionale
, allora il potenziale zero è un numero razionale 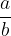 , dove a è un divisore del termine noto
, dove a è un divisore del termine noto 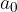 e b un divisore di
e b un divisore di 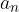 .
.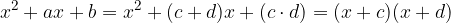
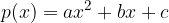
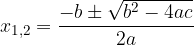
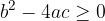 , abbiamo zeri reali.
, abbiamo zeri reali.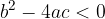 , otteniamo zeri complessi con unità immaginaria.
, otteniamo zeri complessi con unità immaginaria.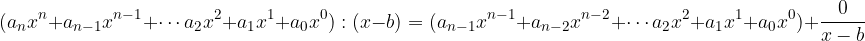
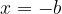
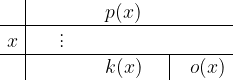
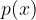 ,mentre nella seconda si riporta il potenziale zero
,mentre nella seconda si riporta il potenziale zero 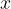 . Dopo una serie di semplici operazioni, otteniamo i coefficienti di un polinomio
. Dopo una serie di semplici operazioni, otteniamo i coefficienti di un polinomio 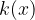 di grado minore e il resto
di grado minore e il resto 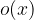 . Se il valore dato è uno zero, allora il resto è
. Se il valore dato è uno zero, allora il resto è