Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





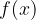 è derivabile ed ammette derivata prima
è derivabile ed ammette derivata prima 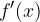 e tale derivata è a sua volta derivabile si definisce derivata seconda di
e tale derivata è a sua volta derivabile si definisce derivata seconda di 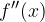 o con
o con 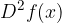
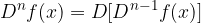
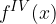 .
.


