Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





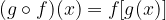
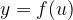 e
e 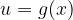 sono tali da definire la funzione composta
sono tali da definire la funzione composta 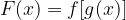 , allora la derivata di F(x) in un punto generico x risulta:
, allora la derivata di F(x) in un punto generico x risulta: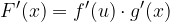
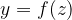 ,
, 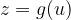 e
e 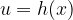 allora si ha:
allora si ha: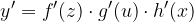
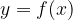 ammette l'inversa
ammette l'inversa 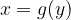 . Se
. Se 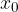 , con derivata
, con derivata 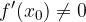 , allora anche
, allora anche 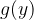 è derivabile in
è derivabile in 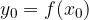 e si ha:
e si ha: