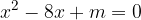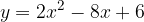matematica
  Libri personalizzati »

Scuole superiori
 
 
 
Prima superiore
 
 
Seconda superiore
 
 
Terza superiore
 
 
Quarta superiore
 
 
Quinta superiore
 
 
Geometria
 
 
Maturità scientifica
 
 
Libri degli insegnanti


fisica
  Libri personalizzati »

Scuole superiori
 
 
 
Meccanica
 
 
Termodinamica
 
 
Oscillazioni e onde
 
 
Elettromagnetismo
 
 
Libri degli insegnanti


inglese
  Libri personalizzati »

Scuole superiori
 
 
 
Grammatica inglese


 
 
Lezioni private e ripetizioni
 
 
Trova un insegnante privato »


 


Sblocca l'accesso ai contenuti
 
Scegli un'opzione:



Gratis
Sblocca il capitolo   "Verifica - 12.1.2018 (4 tracce) "  



Sblocca l'accesso alle soluzioni per gli esercizi di questo capitolo.
Gratis Prezzo: 29.90 €

Continua »
Abbonati a OpenProf     Se non aumenti il ​​voto, restituiremo i soldi!
 


Sblocca l'accesso a tutti gli esercizi.
Disponibile da 2.4916666666667 € / mese.
Continua »
matematica Matematica (2 liceo)
 
Esercizi risolti per capitolo:
 

Verifica - 12.1.2018 (4 tracce)

download pdf
Vedi la teoria »
Equazioni di secondo grado
apri
↓   Mostra documenti teorici [1]   ↓


Le soluzioni passo-passo sono disponibili su:
 
https://it.openprof.com/wb/capitolo:verifica_-_1212018_%284_tracce%29/918/


Esempio 1.

Risolvere la seguente equazione di secondo grado:


    
Esempio 2.

Risolvere la seguente equazione:


    
3.

Verificare se la seguente equazione di secondo grado ammette radici reali senza risolverla e, in caso affermativo, calcolare la somma e il prodotto di tali radici:


    
4.

Calcolare il perimetro di un rettangolo iscritto in una circonferenza di raggio 30 cm, sapendo che la differenza dei suoi lati è di 12 cm.

    
5.

Trovare l'equazione della seguente parabola passante per i punti A, B e C:


    
6.

Rappresentare graficamente la parabola:


    
7.

Risolvere la seguente equazione di secondo grado:


    
8.

Risolvere la seguente equazione di secondo grado:


    

9.

Determinare il valore di k in modo che l'equazione:




abbia una sola radice.

    
10.

Calcolare le lunghezze dei lati di un triangolo rettangolo sapendo che il cateto maggiore supera il cateto minore di 7 cm e che l'ipotenusa lo supera di 8 cm.

    
11.

Scrivere la funzione rappresentata nel seguente grafico:


    
12.

Rappresenta graficamente la parabola


    
13.

Risolvere la seguente equazione di secondo grado:


    
14.

Risolvere la seguente equazione di secondo grado:


    
15.

Determinare per quali valori di k l'equazione:




ammetta radici reali e per quali non ammette soluzioni.

    
16.

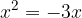
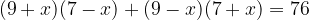
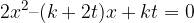
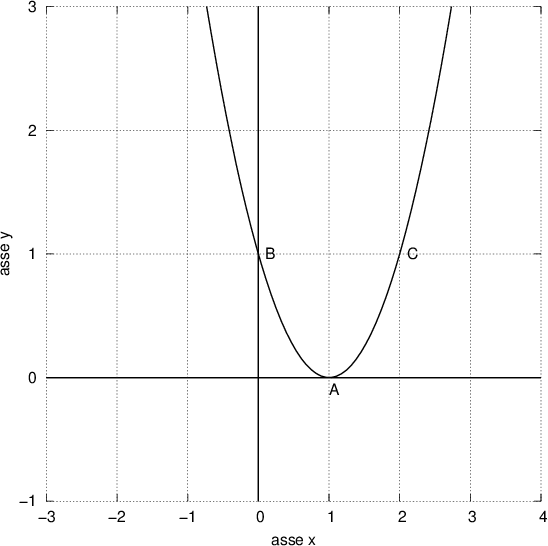
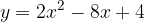
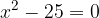
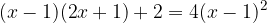
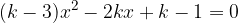
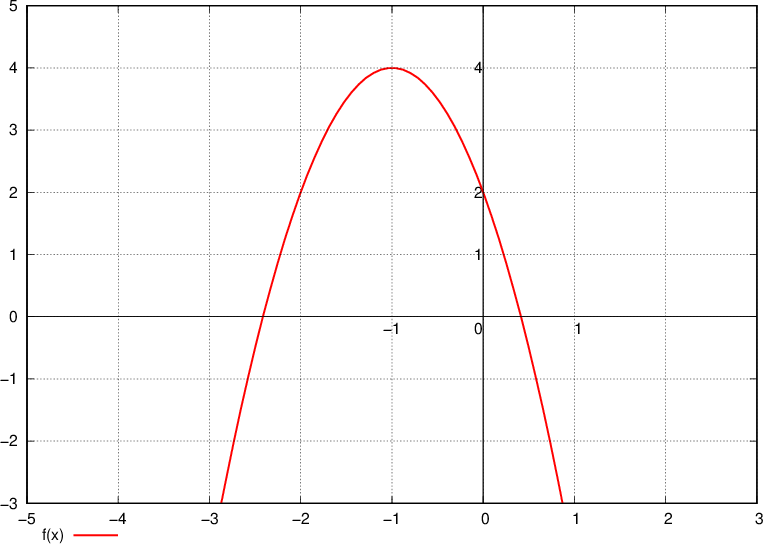
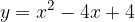
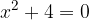
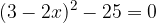
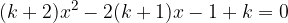
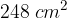L'area di un rettangolo è . Calcolare il perimetro del rettangolo sapendo che la differenza fra la base e l'altezza è .

    
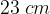17.

Partendo dal grafico trova l'equazione della parabola:


    
18.

Rappresentare graficamente la parabola


    

19.

Risolvere la seguente equazione di secondo grado:


    
20.

Risolvere la seguente equazione di secondo grado:


    
21.

Determinare il valore di m nell'equazione:




in modo che:


  • si abbia una sola radice


  • una radice sia tripla dell'altra


  • una radice valga - 2


    
22.

Individuare tre numeri dispari positivi consecutivi la somma dei cui quadrati è 83.

    
23.

Dato il grafico trova l'equazione della parabola:


    
24.

Rappresenta graficamente la parabola