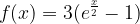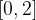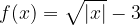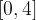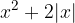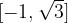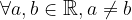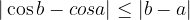Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





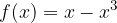
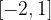
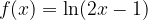
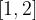
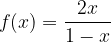
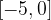
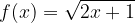
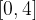
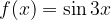
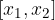
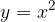

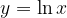

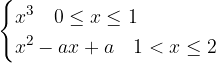
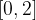
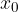 lo soddisfano.
lo soddisfano.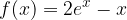
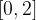
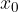 lo soddisfano.
lo soddisfano.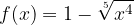
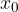 soddisfano il teorema di Lagrange nell’intervallo:
soddisfano il teorema di Lagrange nell’intervallo: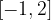
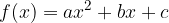
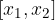 , e trovare il corrispondente valore
, e trovare il corrispondente valore 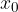 .
.