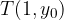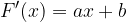matematica
  Libri personalizzati »

Scuole superiori
 
 
 
Prima superiore
 
 
Seconda superiore
 
 
Terza superiore
 
 
Quarta superiore
 
 
Quinta superiore
 
 
Geometria
 
 
Maturità scientifica
 
 
Libri degli insegnanti


fisica
  Libri personalizzati »

Scuole superiori
 
 
 
Meccanica
 
 
Termodinamica
 
 
Oscillazioni e onde
 
 
Elettromagnetismo
 
 
Libri degli insegnanti


inglese
  Libri personalizzati »

Scuole superiori
 
 
 
Grammatica inglese


 
 
Lezioni private e ripetizioni
 
 
Trova un insegnante privato »


 


Sblocca l'accesso ai contenuti
 
Scegli un'opzione:



Gratis
Sblocca il capitolo   "Integrali indefiniti immediati"  



Sblocca l'accesso alle soluzioni per gli esercizi di questo capitolo.
Gratis Prezzo: 29.90 €

Continua »
Abbonati a OpenProf     Se non aumenti il ​​voto, restituiremo i soldi!
 


Sblocca l'accesso a tutti gli esercizi.
Disponibile da 2.4916666666667 € / mese.
Continua »
matematica Esercizi svolti di matematica per la quinta superiore
Esercizi svolti di matematica per la quinta superiore
Esercizi risolti per capitolo:
 

Integrali indefiniti immediati

download pdf
Vedi la teoria »
Integrali indefiniti
apri
↓   Mostra documenti teorici [1]   ↓


Le soluzioni passo-passo sono disponibili su:
 
https://it.openprof.com/wb/capitolo:integrali_indefiniti_immediati/287/


Esempio 1.

Calcola il seguente integrale:


    
Esempio 2.

Calcola il seguente integrale:


    
3.

Calcola il seguente integrale:


    
4.

Risolvi il seguente integrale:


    
5.

Calcola il seguente integrale:


    
6.

Calcola il seguente integrale:


    
7.

Risolvi il seguente integrale:


    
8.

Risolvi il seguente integrale:


    

9.

Risolvi il seguente integrale:


    
10.

Calcola il seguente integrale:


    
11.

Risolvere l'integrale:


    
12.

Risolvere l'integrale:


    
13.

Risolvere l'integrale:


    
14.

Risolvere il seguente integrale e verificare il risultato calcolandone la derivata prima:


    
15.

Risolvere il seguente integrale e verificare il risultato calcolandone la derivata prima:


    
16.

Risolvere il seguente integrale e verificare il risultato calcolandone la derivata prima:


    
17.

Risolvere il seguente integrale e verificare il risultato calcolandone la derivata prima:


    
18.

Trovare l'insieme delle funzioni F che hanno come derivata prima la funzione:


    

19.

Risolvere l'integrale:


    
20.

Risolvere l'integrale:


.

    
21.

Risolvere l'integrale:


    
22.

  • Trovare l'insieme delle funzioni quadratiche la cui derivata prima ha come grafico la bisettrice del secondo e quarto quadrante.


  • Tra le funzioni di tale insieme, scrivere l'equazione e disegnare il grafico della funzione che ha per codominio l'intervallo .


    
23.

Risolvere il seguente integrale e verificare il risultato calcolandone la derivata prima:


    
24.

Risolvere il seguente integrale e verificare il risultato calcolandone la derivata prima:


    
25.

Trovare l'equazione della funzione la cui derivata prima è:




e per la quale vale:


    
26.

Risolvere l'integrale:


    
27.

Risolvere l'integrale:


    
28.

Risolvere l'integrale:


    

29.

Risolvere l'integrale:


    
30.

Risolvere l'integrale:


    
31.

Trovare l'equazione della funzione la cui derivata prima è:




e che passi per il punto di coordinate:


    
32.

Trovare l'equazione della funzione la cui derivata prima è:




e che intersechi l'asse delle ascisse nel punto:


    
33.

Risolvere l'integrale:


    
34.

Risolvere l'integrale:


    
35.

Risolvere l'integrale:


    
36.

Risolvere l'integrale:


    
37.

Risolvere l'integrale:


    
38.

Risolvere l'integrale:


    

39.

Risolvere l'integrale:


    
40.

Risolvere l'integrale:


    
41.

Trovare l'equazione della funzione la cui derivata prima è:




e che intersechi l'asse delle ordinate nel punto:


    
42.

Trovare l'equazione della funzione F sapendo che:


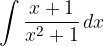
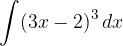
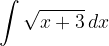
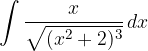
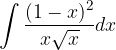
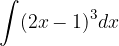
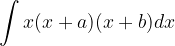
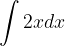
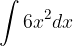
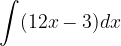
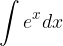
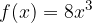
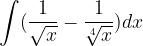
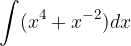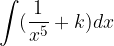
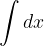
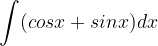
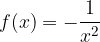
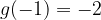
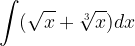
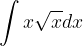
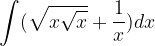
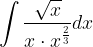
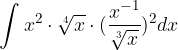
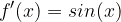
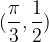
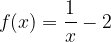
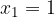
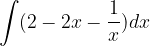
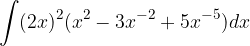
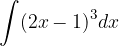
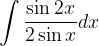
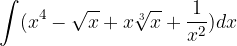
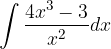
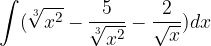
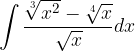
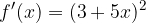
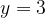
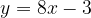  • la retta è una sua tangente nel punto


  • la sua derivata prima è


  • e che passa per l'origine degli assi.


    
43.

Risolvere l'integrale:


    
44.

Risolvere l'integrale:


    
45.

Risolvere l'integrale:


    
46.

Risolvere l'integrale:


    
47.

Risolvere l'integrale:


    
48.

Risolvere l'integrale:


    

49.

Risolvere l'integrale:


    
50.

Risolvere l'integrale:


    
51.

Dimostrare che:


    
52.

Risolvere l'integrale:


    
53.

Risolvere l'integrale:


    
54.

Risolvere l'integrale:


    
55.

Risolvere l'integrale:


    
56.

Risolvere il seguente integrale con l'introduzione di nuove varabili:


    
57.

Risolvere il seguente integrale:


    
58.

Risolvere l'integrale:


    

59.

Dimostrare che vale l'uguaglianza: