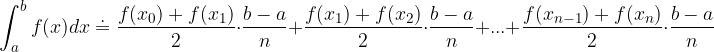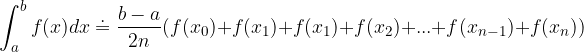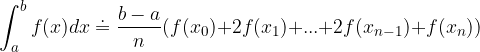Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





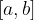 in n parti uguali:
in n parti uguali: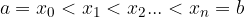
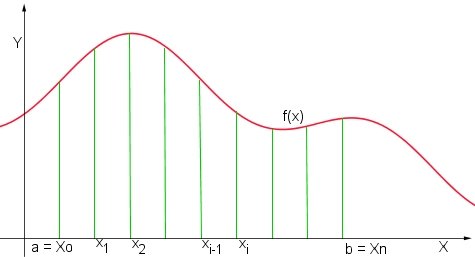
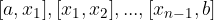
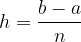
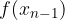 e
e 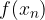 e altezza
e altezza 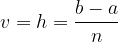
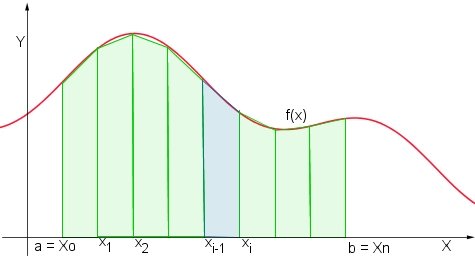
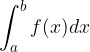 è dato dalla somma delle aree di tutti i trapezi:
è dato dalla somma delle aree di tutti i trapezi: