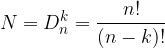Il calcolo combinatorio può essere studiato mettendolo in relazione con le funzioni. Come sappiamo, una funzione è una relazione che associa ad ogni elemento di un insieme (dominio) uno e un solo elemento di un secondo insieme (codominio). Possiamo distinguere tra tre tipi di funzioni:
funzioni iniettive
funzioni suriettive
funzioni biunivoche
Vediamo come il calcolo combinatorio può essere messo in relazione ad ognuno dei tre tipi di funzione.
Una funzione è iniettiva quando ad ogni elemento del dominio corrisponde un diverso elemento del codominio. Per una funzione iniettiva è possibile che alcuni elementi del codominio non siano raggiunti da nessun elemento del dominio.
Nell'immagine seguente vediamo un esempio di funzione iniettiva, poiché ognuna di tre spose (1° insieme) sceglie per il proprio matrimonio un distinto tipo di fiore (2° insieme). Possiamo anche vedere che il tulipano non viene scelto da nessuna delle spose.
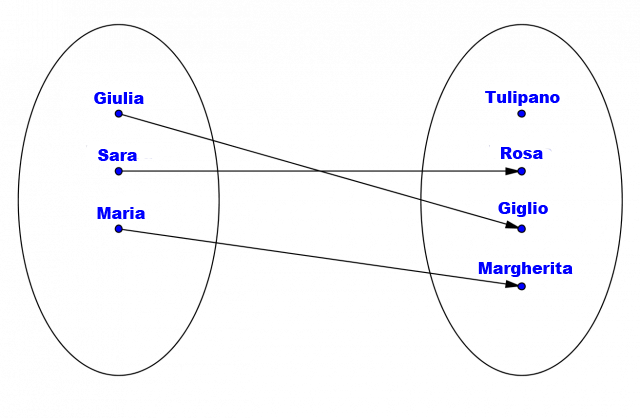
Esempio di funzione iniettiva
Nell'esempio è rappresentata una sola combinazione tra spose e fiori, ma naturalmente esistono molte altre combinazioni. Vediamo le altre possibili combinazioni con un esempio.
Se dunque k è il numero di elementi di un primo insieme e n è il numero di elementi di un secondo insieme, il numero totale di combinazioni è dato dalla formula:
Tale numero è esattamente uguale al numero di funzioni iniettive che abbiano un dominio costituito da k elementi e un codominio costituito da n elementi (con k < n).
Una funzione è suriettiva quando ad ogni elemento del codominio corrisponde almeno un elemento del dominio. Per una funzione suriettiva è possibile quindi che alcuni elementi del dominio raggiungano lo stesso elemento del codominio.
Nell'immagine seguente vediamo un esempio di funzione suriettiva, poiché ogni tipo di fiore (2° insieme) viene scelto da almeno una delle spose (1° insieme). Possiamo anche vedere che il tulipano viene scelto da due delle spose e lo stesso accade per il giglio.
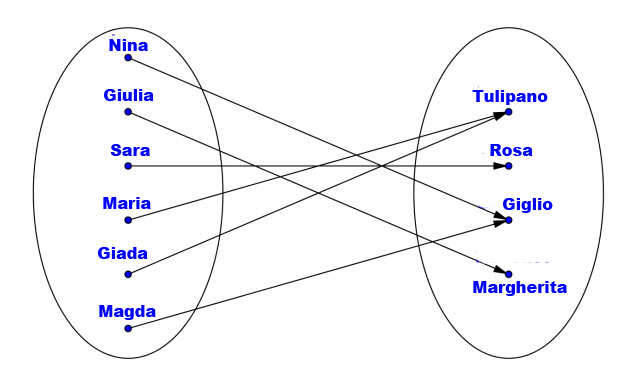
Esempio di funzione suriettiva
Nell'esempio è rappresentata una sola combinazione tra spose e fiori, ma naturalmente esistono molte altre combinazioni. Vediamo le altre possibili combinazioni con un esempio.
Il numero di disposizioni con ripetizione non è esattamente uguale al numero di funzioni suriettive che abbiano un dominio costituito da k elementi e un codominio costituito da n elementi, ma solo alcune delle disposizioni rappresenteranno tali funzioni.
Una funzione è biunivoca quando è iniettiva e suriettiva allo stesso tempo, ovvero quando ad ogni elemento del dominio corrisponde esattamente un elemento del codominio. Per una funzione biunivoca il numero di elementi del dominio è uguale al numero di elementi del codominio.
Nell'immagine seguente vediamo un esempio di funzione biunivoca, poiché ogni sposa (1° insieme) sceglie un tipo di fiore distinto (2° insieme). Possiamo anche vedere che il numero di tipologie di fiori che si possono scegliere è esattamente uguale al numero di spose.
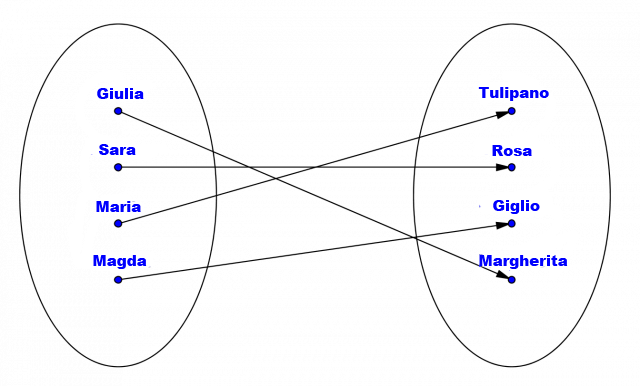
Esempio di funzione biunivoca
Nell'esempio è rappresentata una sola combinazione tra spose e fiori, ma naturalmente esistono molte altre combinazioni. Vediamo le altre possibili combinazioni con un esempio.
Il numero di permutazioni coincide con il numero di funzioni biunivoche perché abbiamo due insiemi con lo stesso numero di elementi e ad ogni elemento del primo insieme (dominio) corrisponde un solo elemento del secondo insieme (codominio)
