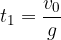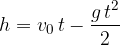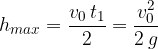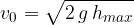Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti




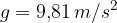
 :
:
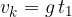
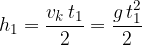
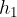 :
: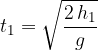
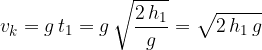
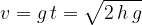
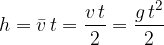
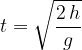
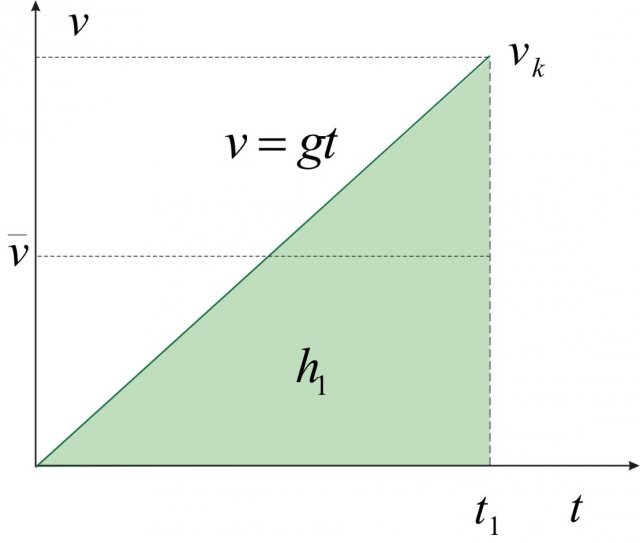
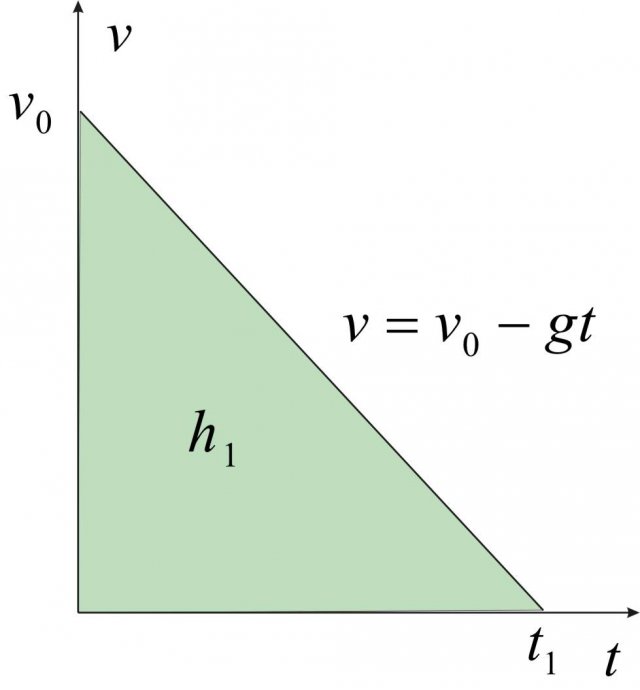
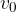 diversa da zero (vedi Figura 2). Anche le equazioni e i grafici di questo caso sono già state studiate nel capitolo
diversa da zero (vedi Figura 2). Anche le equazioni e i grafici di questo caso sono già state studiate nel capitolo 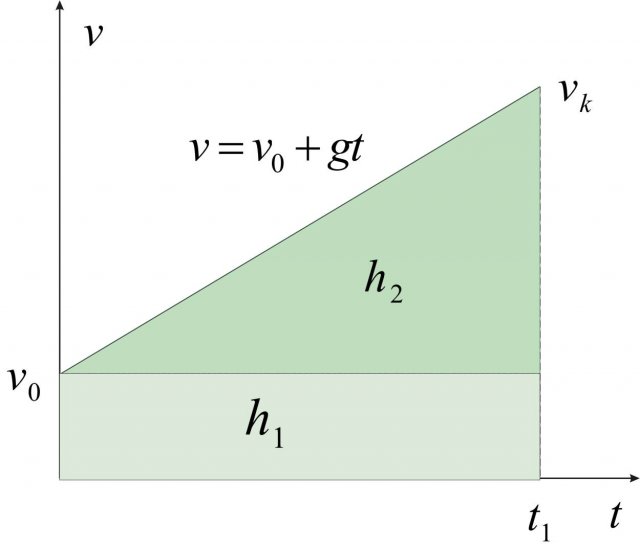
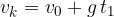
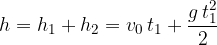
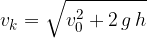
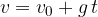
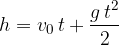
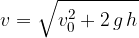
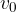 . In una prima parte del moto, l'accelerazione di gravità di comporta come una decelerazione, finchè a un certo istante
. In una prima parte del moto, l'accelerazione di gravità di comporta come una decelerazione, finchè a un certo istante 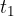 raggiunge un'altezza massima di
raggiunge un'altezza massima di  in cui
in cui 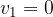 .
.
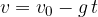
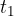 in cui
in cui 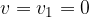 è:
è: