Abbiamo visto che le equazioni di secondo grado in una sola variabile x, ridotte in forma normale, presentano generalmente la forma standard:
Esistono tuttavia altre forme non standard che possiamo così classificare in base al valore dei coefficienti:
Inoltre, quando un'equazione presenta la variabile x al denominatore di una frazione, abbiamo un altro tipo di equazione non standard, detta equazione frazionaria.
Equazione monomia
L'equazione monomia si presenta nella forma:
con 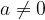 .
.
E' chiaro che l'unico valore di x che annulla il primo membro è:
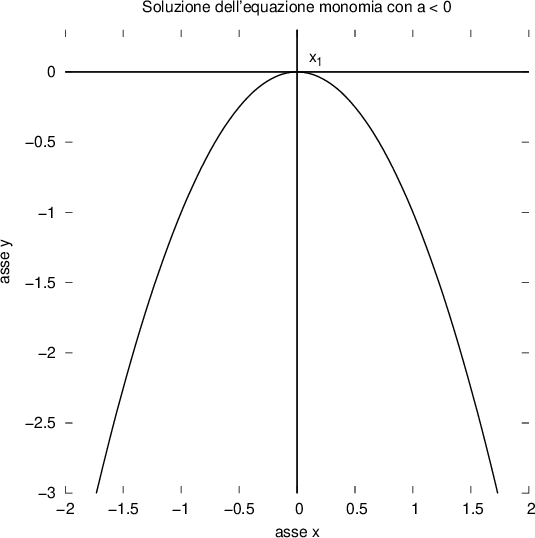
Se consideriamo la funzione:
Poiché per 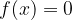 , abbiamo visto che l'unica soluzione possibile è:
, abbiamo visto che l'unica soluzione possibile è:
il grafico della funzione sarà una parabola il cui vertice interseca l'origine degli assi cartesiani, ovvero il punto in cui sia l'ascissa che l'ordinata sono uguali a zero:
Equazione spuria
L'equazione spuria si presenta nella forma:
con 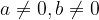 .
.
Per risolvere l'equazione, mettiamo in evidenza il fattore comune ai due monomi, ovvero x:
Perché l'uguaglianza sia valida, deve verificarsi una delle seguenti condizioni, o entrambe:
La seconda condizione è un'equazione di primo grado che avrà come sola radice:
Dunque un'equazione spuria avrà sempre due radici distinte, di cui una è nulla:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Se consideriamo la funzione:
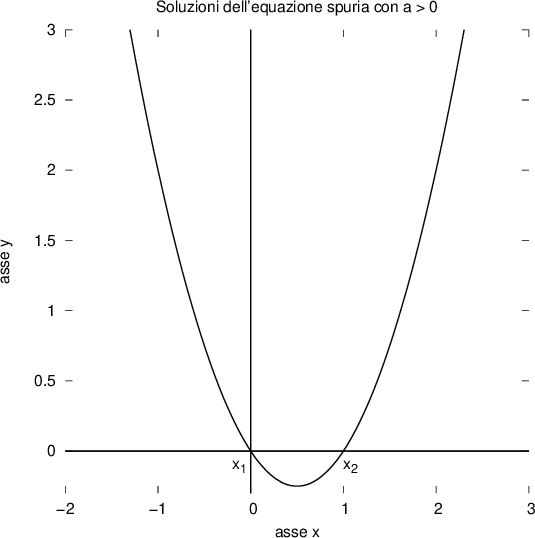
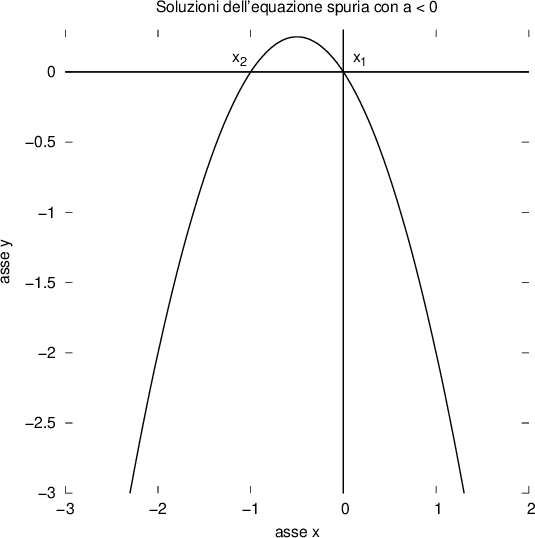
Poiché per 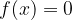 , abbiamo due possibili radici, di cui una è uguale a zero, il grafico della funzione sarà una parabola che interseca l'asse delle X in due punti, di cui uno è l'origine degli assi:
, abbiamo due possibili radici, di cui una è uguale a zero, il grafico della funzione sarà una parabola che interseca l'asse delle X in due punti, di cui uno è l'origine degli assi:
Equazione pura
L'equazione pura si presenta nella forma:
con 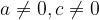 .
.
Per risolvere l'equazione, portiamo il termine noto al secondo membro e poi dividiamo entrambi i membri per a:
Si tratta ora di trovare quel numero reale che elevato al quadrato dia come risultato 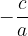 .
.
Possono verificarsi due condizioni:
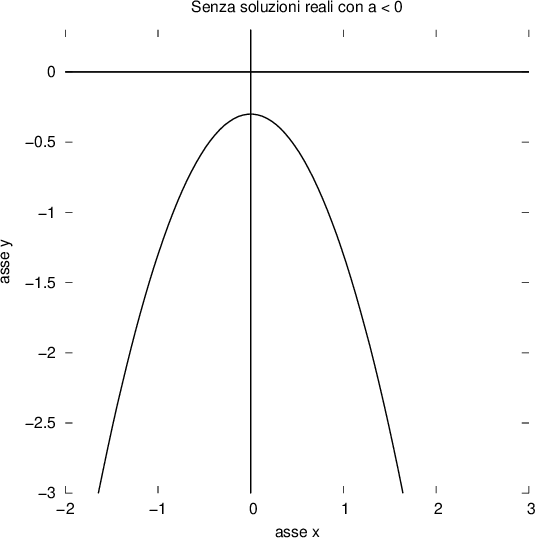
Forma senza soluzioni
Per 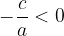 non esistono soluzioni reali:
non esistono soluzioni reali:
ovvero non esiste alcun numero reale il cui quadrato dia un numero negativo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
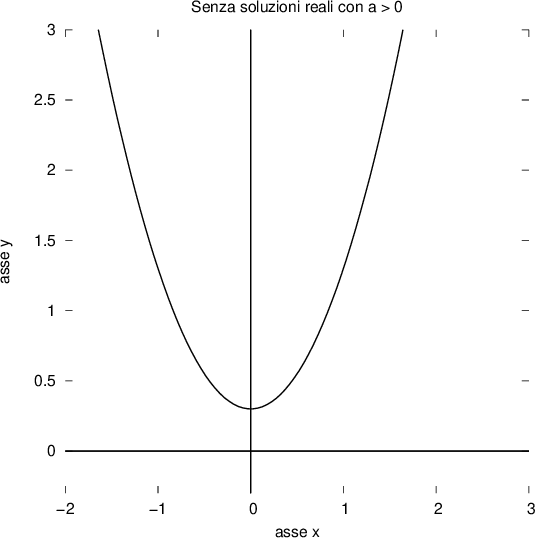
Se consideriamo la funzione:
con 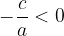
il grafico della funzione sarà una parabola che non interseca l'asse delle X:
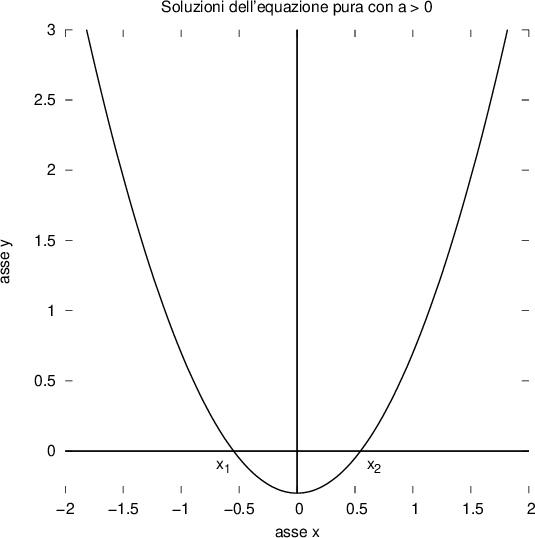
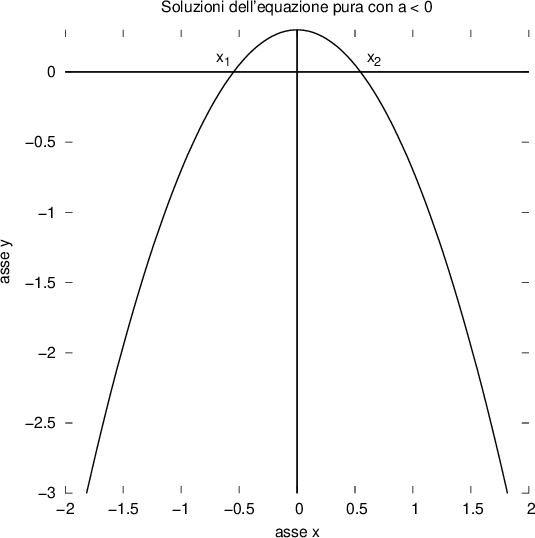
Forma risolvibile
Per 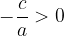 esistono due soluzioni reali distinte:
esistono due soluzioni reali distinte:
ovvero esistono due numeri reali, tra loro opposti, che elevati al quadrato danno come risultato 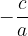
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Se consideriamo la funzione:
con 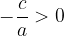
il grafico della funzione sarà una parabola simmetrica rispetto all'asse delle Y e che interseca l'asse delle X in due punti con ascisse opposte, ovvero con 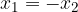 :
:
Equazioni frazionarie
Le equazioni frazionarie sono equazioni che presentano l'incognita x anche al denominatore di frazioni algebriche. Ovviamente, in tal caso, prima di risolvere l'equazione bisogna prima escludere tutti i valori della x che annullerebbero i denominatori.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Le equazioni frazionarie si risolvono come le equazioni intere se moltiplichiamo prima entrambi i membri dell'uguaglianza per un multiplo comune dei denominatori.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »




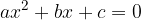
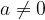
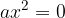
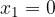
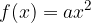
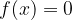 , abbiamo visto che l'unica soluzione possibile è:
, abbiamo visto che l'unica soluzione possibile è: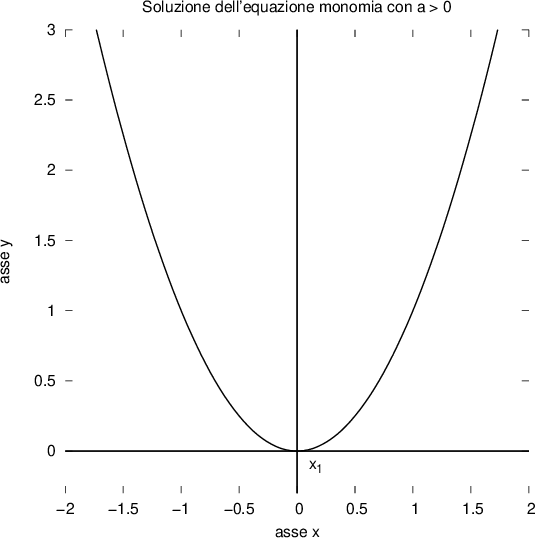
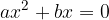
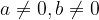 .
.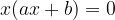
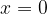
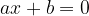
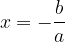
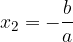
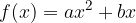
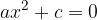
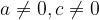 .
.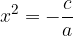
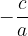 .
.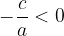 non esistono soluzioni reali:
non esistono soluzioni reali: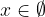
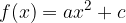
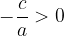 esistono due soluzioni reali distinte:
esistono due soluzioni reali distinte: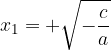
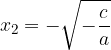
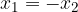 :
: